[선형대수] 03 - 벡터의 노름과 거리

들어가며

이번 포스팅은 고차원 공간에서의 거리 개념을 다룬다.
벡터의 노름과 다양한 거리 측정 방법들을 이해하고, AI/ML에서 어떻게 활용되는지 알아보려 한다.

Norm

---

1. Vector Norm 이란?

벡터 Norm은 벡터의 크기(길이)를 측정하는 함수로, 고차원 공간에서 벡터의 절대적인 크기를 나타낸다.

• Norm은 절대값/길이를 의미하므로 항상 0 이상 (양수)
• Norm은 Vector -> Scalar로 바꾼다.
• Norm은 길이의 일반화된 개념
• Norm 종류
  • L1 Norm (맨해튼 노름)
  • L2 Norm (유클리드 노름)
  • L∞ Norm (최대 노름)

Vector Norm

왜 Norm이 중요한가?

• 벡터 비교: 서로 다른 벡터의 크기를 정량적으로 비교
• 정규화: 벡터를 단위 길이로 만들어 방향만 보존
• 거리 계산: 벡터 간 거리 측정의 기초
• 최적화: 손실 함수에서 정규화 항으로 활용

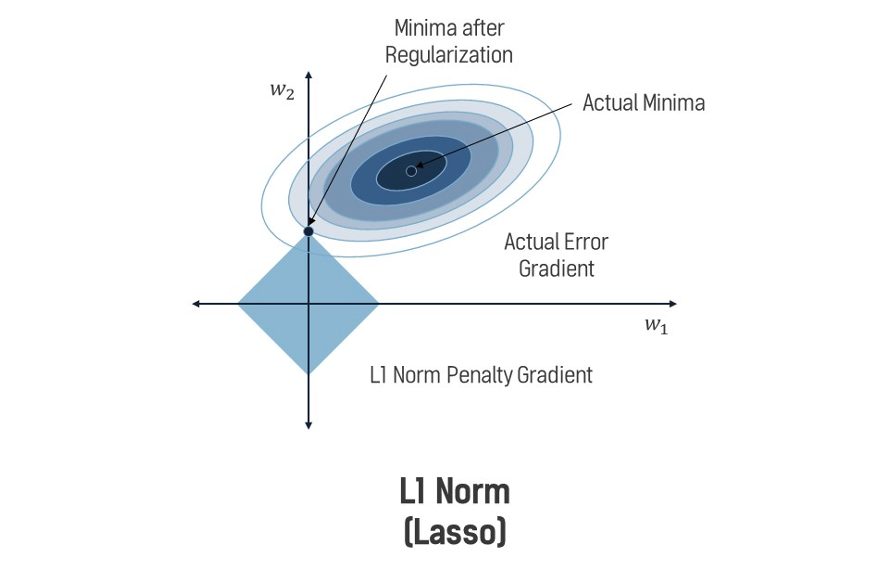
2. L1 Norm (맨해튼 노름)

L1 Norm (맨해튼 노름)은 벡터 성분 절댓값의 합으로 정의되며, 벡터의 길이를 계산하는 방법 중 하나다.

L1 Norm

기하학적 의미

• 벡터의 크기를 각 성분의 절댓값 합으로 측정
• 원점에서 해당 점까지 격자 형태로 이동하는 경로의 총 거리
• 다이아몬드 형태의 등거리선(norm ball) 형성

주요 특징

• 희소성(Sparsity) 유도: 많은 가중치를 정확히 0으로 만듦
• Lasso 회귀: 자동 변수 선택 효과
• 아웃라이어에 강건: 극값의 영향 적음

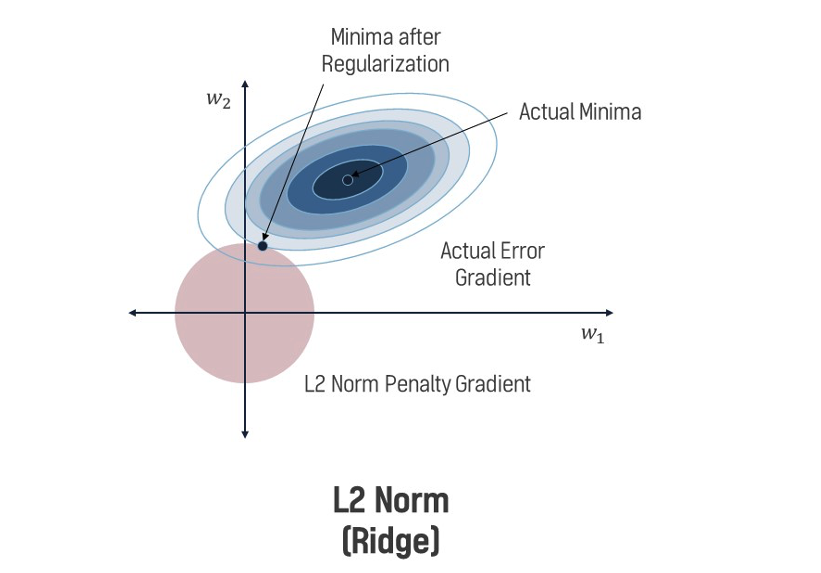
3. L2 Norm (유클리드 노름)

L2 Norm (유클리드 노름)은 벡터 성분의 제곱합의 제곱근으로 정의되며, 일반적인 거리 개념을 나타낸다.

L2 Norm

기하학적 의미

• 벡터의 크기를 성분의 제곱합의 제곱근으로 측정
• 원점에서 해당 점까지의 직선 거리 (최단 거리)
• 원 형태의 등거리선(norm ball) 형성

주요 특징

• 미분 가능: 비선형 최적화에 적합
• Ridge 회귀: 가중치 수축으로 과적합 방지
• 아웃라이어에 민감: 극값의 영향 큼

Distance

---

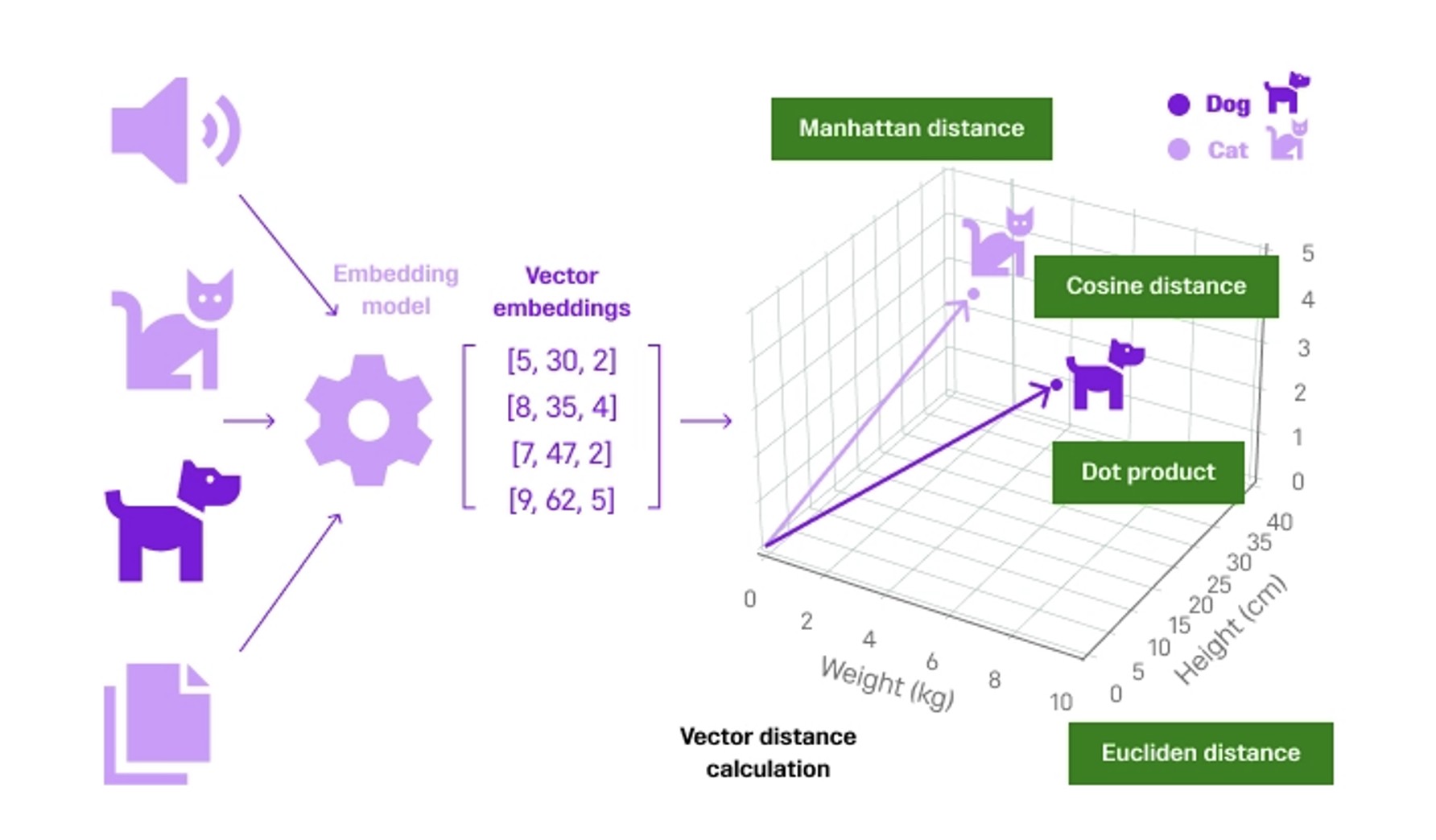
1. Vector Distance 란?

두 벡터 간의 차이나 유사성을 측정하는 함수로, 고차원 공간에서 데이터 포인트 간의 관계를 정량화한다.

• 거리는 두 벡터 -> 스칼라로 변환
• 항상 0 이상의 값을 가지며, 같은 벡터 간의 거리는 0
• 대칭성: d(a, b) = d(b, a)
• 거리 종류
  • 유클리드 거리 (Euclidean Distance)
  • 맨해튼 거리 (Manhattan Distance)
  • 코사인 거리/유사도 (Cosine Distance/Similarity)

Vector Distance

왜 Distance가 중요한가?

• 데이터 분류: KNN, 클러스터링에서 유사한 데이터 그룹핑
• 추천 시스템: 사용자/아이템 간 유사도 계산
• 이상 탐지: 정상 데이터와의 거리로 이상값 검출
• 차원 축소: 거리 보존을 통한 데이터 압축

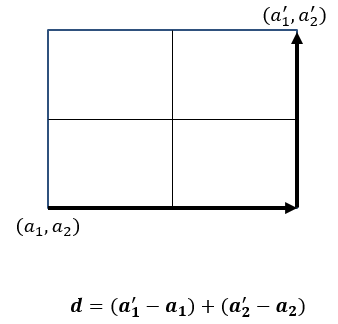
2. 맨해튼 거리 (Manhattan Distance)

맨해튼 거리는 L1 Norm을 기반으로 격자 형태로 이동하는 거리를 측정하며, 택시 거리라고도 불린다.

맨해튼 거리

기하학적 의미

• 두 점 간의 격자 경로 거리 (수직+수평 이동)
• 맨해튼 도로망에서 택시가 이동하는 거리와 동일
• 대각선 이동 불가능한 환경의 거리

주요 특징

• 계산 효율: 제곱근 연산 불필요
• 희소성: 차이가 작은 차원 무시
• 로버스트: 아웃라이어에 덜 민감 (절댓값만 사용하기에)

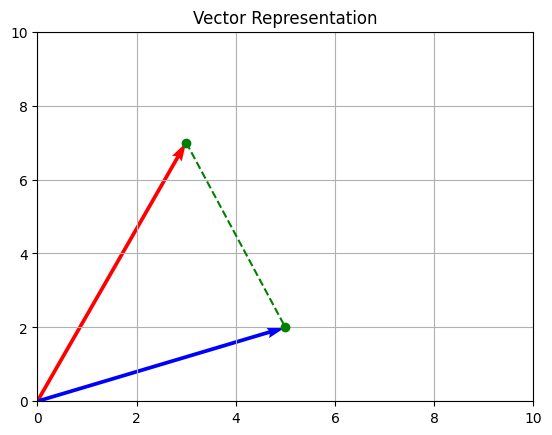
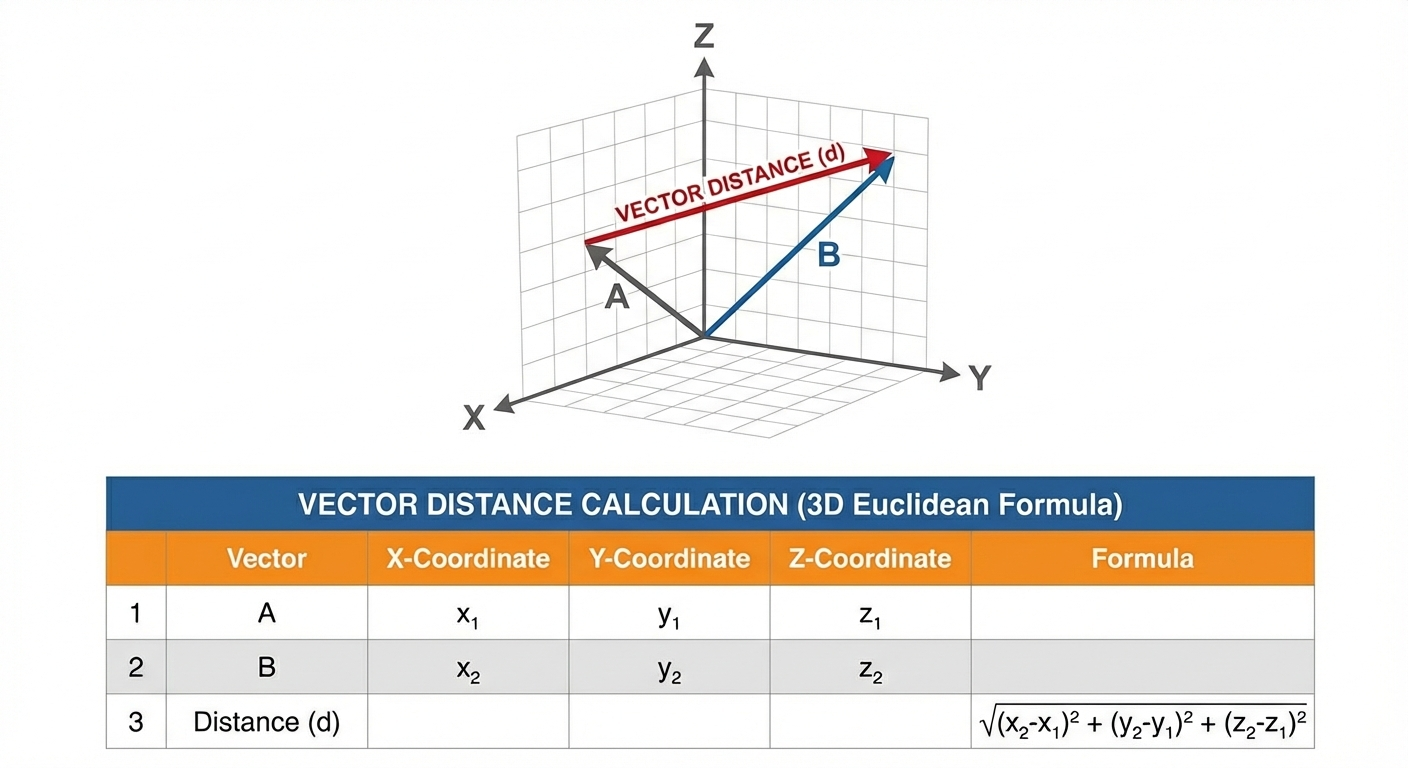
3. 유클리드 거리 (Euclidean Distance)

유클리드 거리는 L2 Norm을 기반으로 두 벡터 간의 직선 거리를 측정하며, 가장 직관적인 거리 개념이다.

유클리드 거리

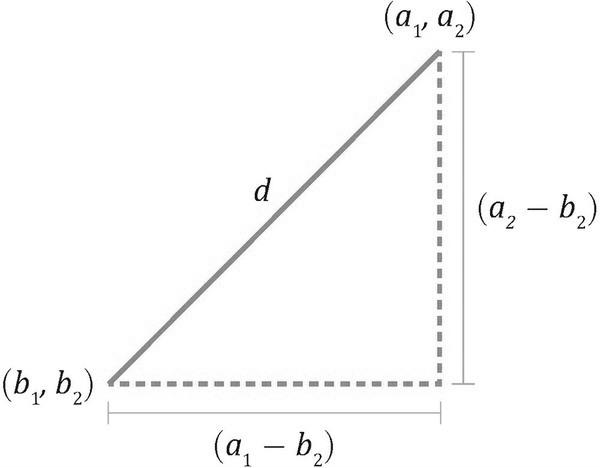
기하학적 의미

• 두 점 간의 최단 직선 거리 (피타고라스 정리)
• 2차원에서는 삼각형의 빗변 길이와 동일
• 고차원에서도 직선 거리의 일반화

주요 특징

• 직관적: 일반적인 물리적 거리와 일치 (직선 거리를 사용하기에)
• 회전 불변: 좌표계 회전에도 거리 보존 (유클리드 성질을 따르기에)
• 제곱 거리: 연산 효율을 위해 제곱근 생략 가능 (대소 비교만 필요하기에)

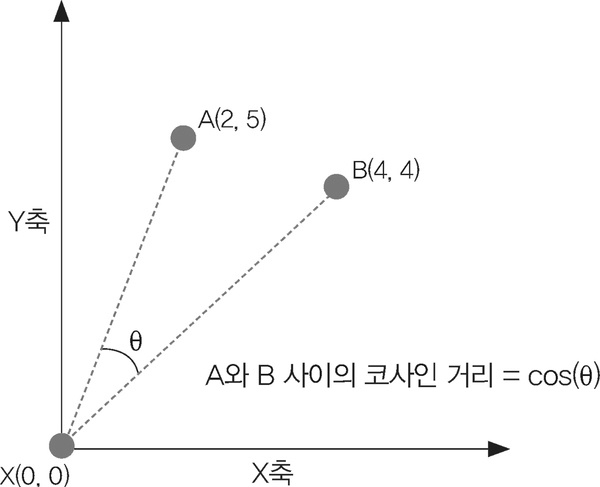
4. 코사인 유사도 (Cosine Similarity)

코사인 유사도는 벡터 간 각도를 측정하여 방향의 유사성을 나타내며, 벡터 크기에 무관한 유사도를 제공

코사인 거리

기하학적 의미

• 두 벡터가 이루는 각도의 코사인 값
• -1(반대)부터 1(동일) 사이의 값
• 벡터의 방향만 고려, 크기 무시

주요 특징

• 크기 무관: 벡터 길이에 영향받지 않음 (정규화 후 내적을 계산하기에)
• 문서 유사도: NLP에서 텍스트 유사도 측정 (방향만 비교하기에)
• 추천 시스템: 사용자 선호도 패턴 분석 (상대적 선호도를 비교하기에)