[선형대수] 02 - PCA (주성분 분석)

들어가며

이번 포스팅은 AI/ML에서 핵심적으로 사용되는 PCA(주성분 분석)를 선형대수 관점에서 정리했다.
이전 포스팅에서 다룬 고유값과 고유벡터가 실제로 어떻게 활용되는지 확인할 수 있다.

주성분 분석 (PCA)

---

1. 차원의 저주 (Curse of Dimensionality)

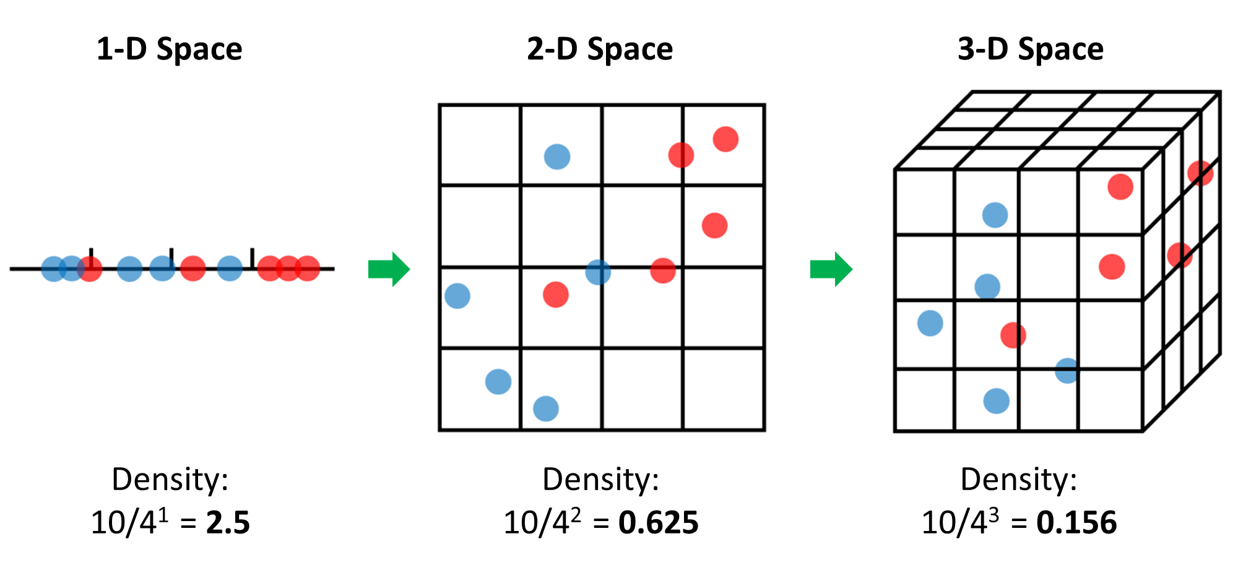
차원의 저주란 데이터의 차원이 증가할수록 데이터가 희소해지고, 그로 인해 성능이 저하되는 현상이다.

차원의 저주

• 위 그림처럼 차원이 증가할수록 빈 공간이 많아진다.
• 즉, 정보가 없는 공간이기 때문에 빈 공간이 많을수록 학습시켰을 때 모델 성능이 저하될 수 밖에 없다.
• 주의할 점은 변수가 증가한다고 반드시 차원의 저주가 발생하는 것은 아니다.
• 관측지보다(rows) 변수 수가 많아지는 경우에 차원의 저주 문제가 발생하는 것이다.

2. PCA 란?

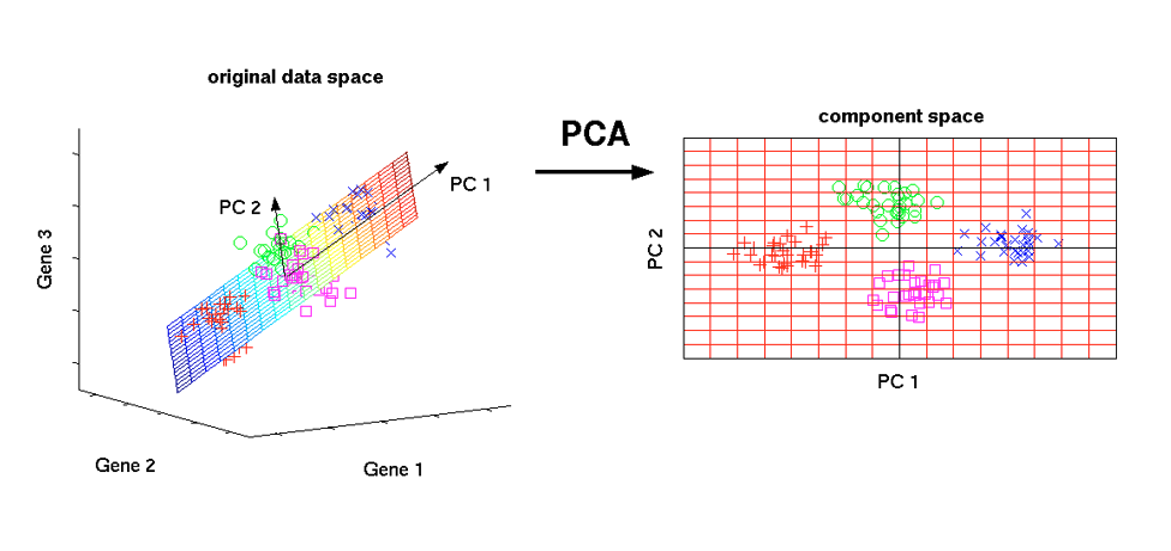
PCA는 고차원 데이터에서 가장 중요한 방향(주성분)을 찾아 저차원으로 투영하는 차원 축소 기법이다.

주성분 찾기

PCA의 동작 원리

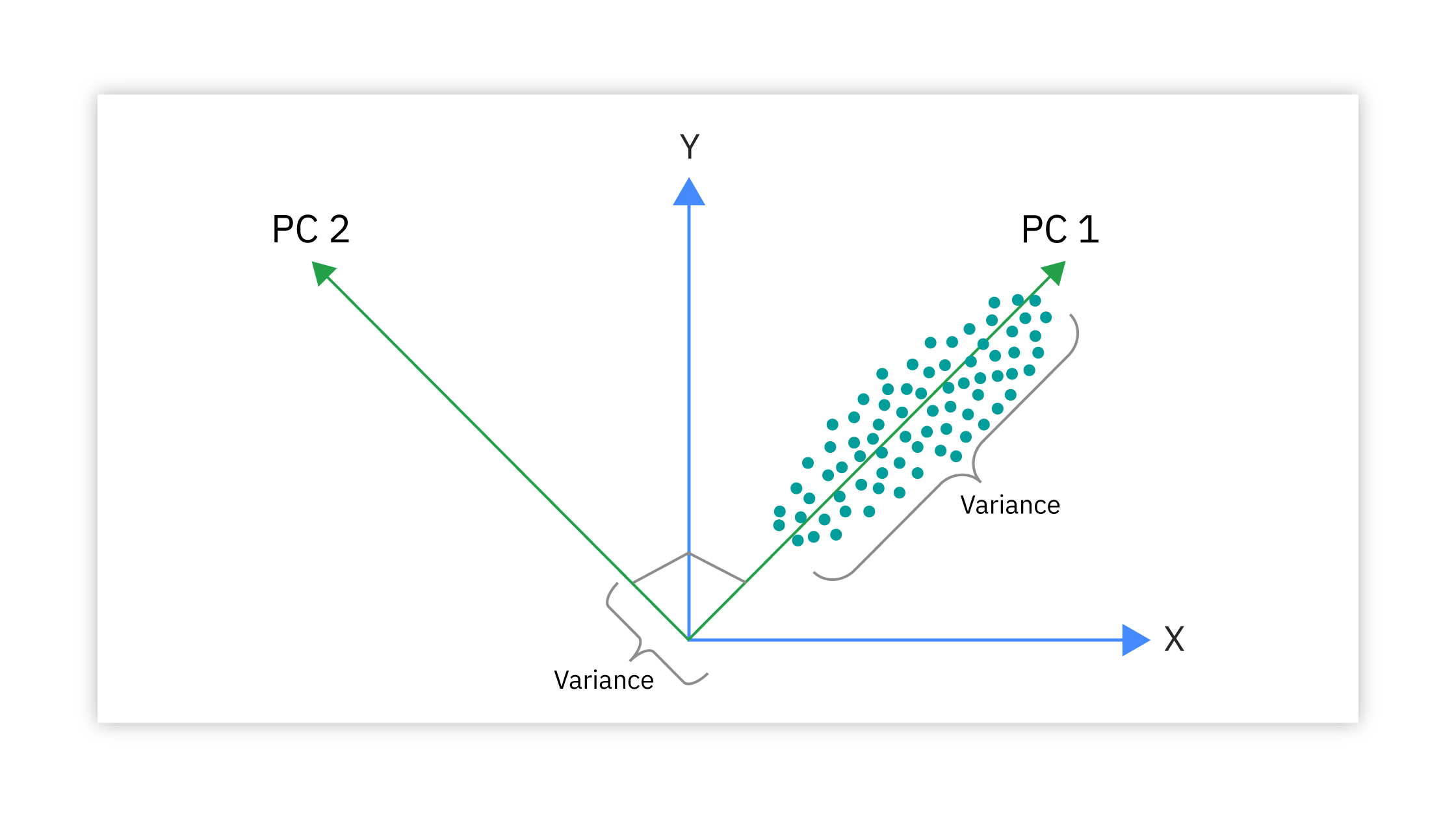
• 데이터의 분산이 가장 큰 방향을 찾아서 그 방향으로 데이터를 투영
• 첫 번째 주성분: 데이터 분산이 최대인 방향
• 두 번째 주성분: 첫 번째와 수직이면서 분산이 두 번째로 큰 방향
• 세 번째 주성분: 앞의 두 방향과 수직이면서 분산이 세 번째로 큰 방향

PCA가 해결하는 문제

• 정보 손실 최소화: 가장 중요한 정보만 남기고 나머지는 제거
• 시각화 가능: 고차원 데이터를 2D/3D로 변환하여 그래프로 표현
• 노이즈 제거: 중요하지 않은 방향의 노이즈를 자동으로 필터링
• 연산 효율성: 차원 수 감소로 계산 속도 향상

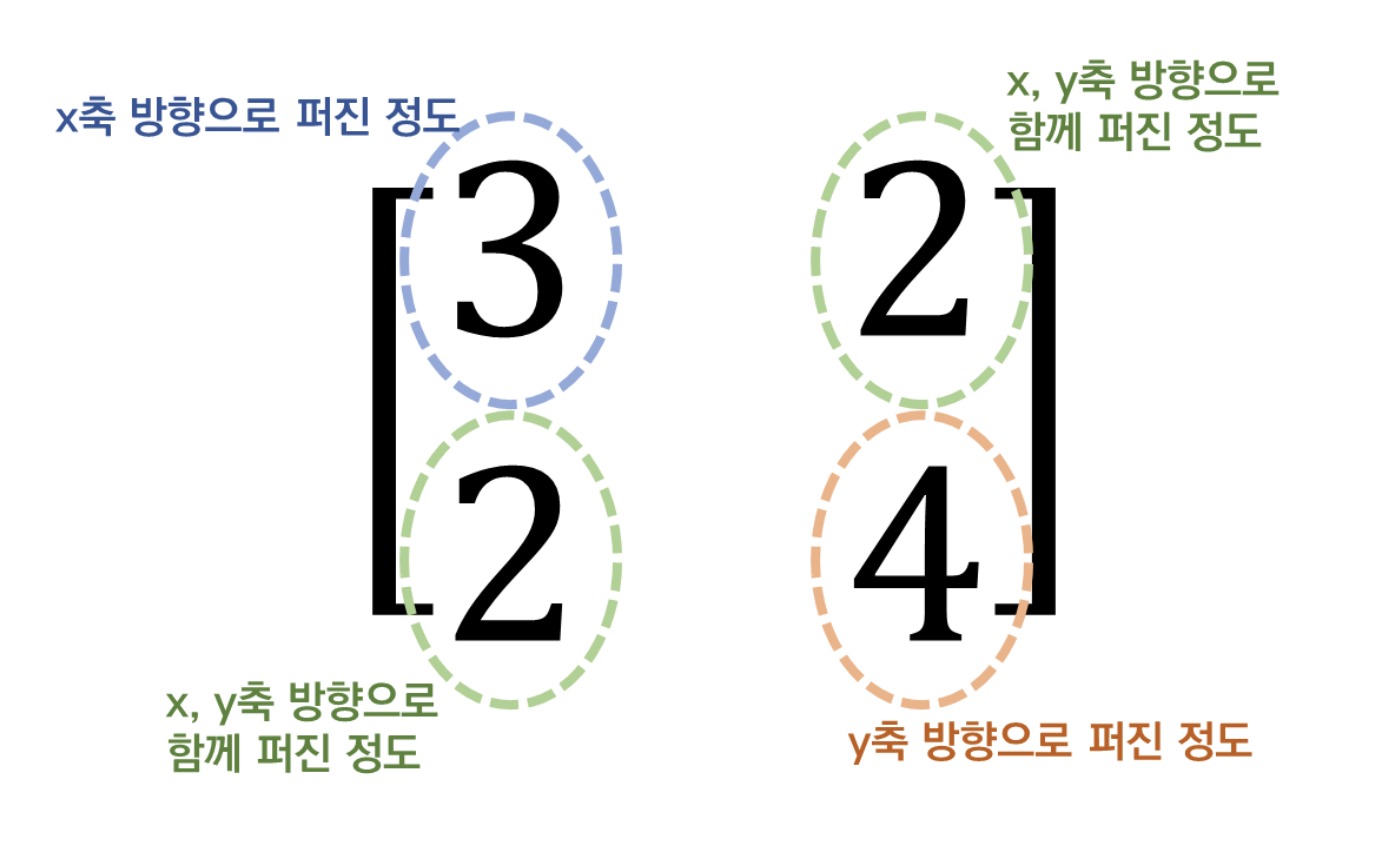
3. 공분산 행렬

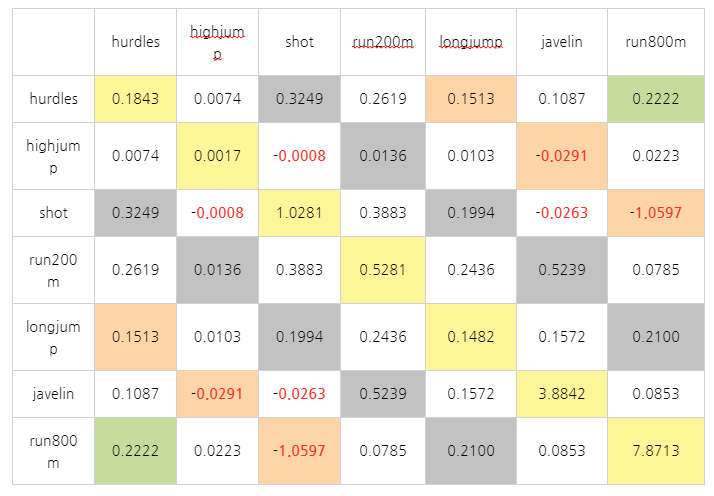
공분산 행렬은 변수들 간의 관계를 수치화하여, 데이터 분산이 가장 큰 방향을 찾기 위한 행렬이다.

공분산 행렬

공분산 행렬의 개념

• 공분산: 두 변수가 함께 변하는 정도를 나타내는 값
• 공분산 행렬: 모든 변수 쌍의 공분산을 모아놓은 정사각 행렬
• 대각선 요소: 각 변수의 분산 (자기 자신과의 공분산)
• 비대각선 요소: 서로 다른 변수 간의 공분산

공분산

공분산 행렬과 고유벡터

• 공분산 행렬의 고유벡터 = 주성분 방향
• 공분산 행렬의 고유값 = 각 주성분 방향의 분산 크기
• PCA 적용: 데이터 분산이 최대/최소인 방향이 바로 공분산 행렬의 고유벡터

왜 고유값/고유벡터가 중요한가?

• 자동으로 최적 방향 찾기: 고유벡터는 데이터 분산이 최대가 되는 방향을 자동으로 계산
• 중요도 순서: 고유값이 큰 순서대로 정렬하면 가장 중요한 주성분부터 순서대로 획득
• 수학적 보장: 고유벡터들은 서로 수직(직교)이므로 중복되지 않는 독립적인 정보 제공
• 효율적 계산: 복잡한 최적화 문제를 선형대수의 고유값 분해로 간단히 해결

왜 공분산 행렬이 중요한가?

• PCA(주성분 분석)의 목표가 분산이 가장 큰 방향(고유 벡터)을 찾는 것이기 때문
• 공분산 행렬을 통해 데이터의 분산 구조를 한눈에 요약할 수 있어, PCA가 최적 방향을 찾는 근거가 된다.

4. 설명된 분산의 비율

설명된 분산의 비율은 각 주성분이 전체 데이터 변동성의 몇 퍼센트를 설명하는지 나타내는 중요한 지표다.

분산 기여도 계산

• 개별 기여도: 각 고유값 ÷ 전체 고유값 합
• 누적 기여도: 첫 번째부터 k번째까지 주성분의 기여도 합

\[\text{설명된 분산 비율} = \frac{\lambda_i}{\sum_{j=1}^{p} \lambda_j} \times 100\%\] \[\text{누적 설명된 분산} = \frac{\sum_{j=1}^{k} \lambda_j}{\sum_{j=1}^{p} \lambda_j} \times 100\%\]

실제 적용 예시

• 1차 주성분: 65% → 데이터 변동의 65%를 설명
• 2차 주성분: 20% → 추가로 20% 설명 (누적 85%)
• 3차 주성분: 10% → 추가로 10% 설명 (누적 95%)
• 4차 이후: 5% → 노이즈로 간주하고 제거

몇 개의 주성분을 선택할까?

• 임계값(threshold): 누적 기여도가 80% 이상이 되는 지점까지 선택 (보통 95% 선택)
• Kaiser 기준: 고유값이 1보다 큰 주성분만 선택
• Scree Plot: 급격한 감소가 끝나는 지점(elbow point)에서 선택
• 도메인 지식: 해석 가능성과 실용성을 고려하여 결정

5. PCA 한계와 SVD 활용 이유

PCA는 강력한 차원 축소 기법이지만, 한계가 존재하며, 이를 보완하기 위해 SVD를 활용하기도 한다.

PCA의 한계

• 선형성 가정: PCA는 데이터의 선형 관계를 전제로 하므로, 비선형 패턴을 충분히 반영하지 못한다.
• 스케일 민감: 변수들의 단위나 스케일이 다르면, 공분산 계산 결과가 왜곡될 수 있다.
• 해석의 어려움: 주성분은 기존 변수의 선형 조합이기 때문에, 실제 의미를 직관적으로 해석하기 어렵다.
• 노이즈에 민감: 분산이 작은 중요한 신호가 노이즈로 취급될 수 있다.

SVD를 활용하는 이유

• 모든 행렬 적용 가능: 공분산 행렬은 정방행렬만 가능하지만, SVD는 직각 행렬에도 적용 가능하다.
• 수치적 안정성: 큰 데이터셋에서도 계산이 안정적이며, 공분산 행렬을 직접 계산하지 않아도 된다.
• 직관적 차원 축소
  • SVD로 분해된 행렬의 특이값과 특이벡터를 활용하면
  • PCA와 동일하게 주성분 방향과 분산 정보를 얻을 수 있다.