[선형대수] 01 - 고유값과 SVD

들어가며

이번 포스팅은 AI/ML에서 자주 쓰이는 선형대수의 핵심 개념인 고유값, 고유벡터와 SVD를 정리했다.

고유값과 고유벡터 (Eigenvalue & Eigenvector)

---

1. 행렬과 벡터

고유값과 고유벡터에 대한 내용을 다루기전에 복습차원에서 행렬과 벡터의 기본 개념을 먼저 정리

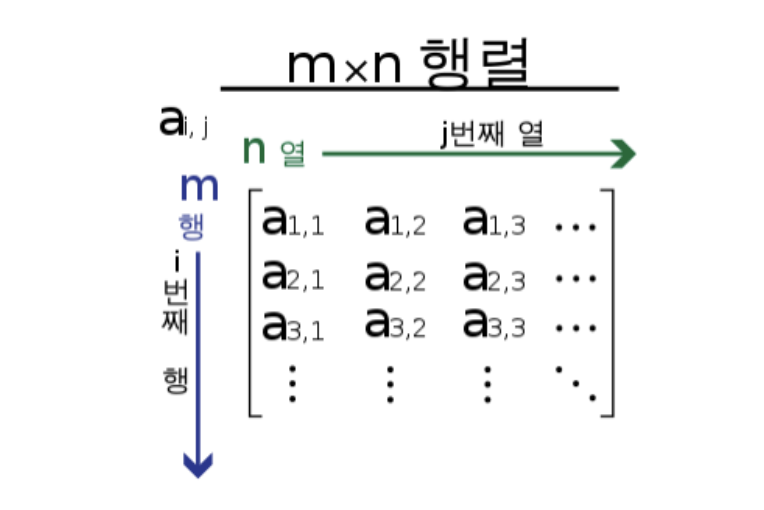
행렬 (Matrix)

• 행렬은 수를 직사각형 형태로 배열한 구조로, 선형변환을 나타내며, 데이터 변환을 담당한다.
• 정방행렬: 행의 개수와 열의 개수가 정사각형 모양의 행렬을 말함
• 선형변환: 벡터를 다른 벡터로 변환하는 역할

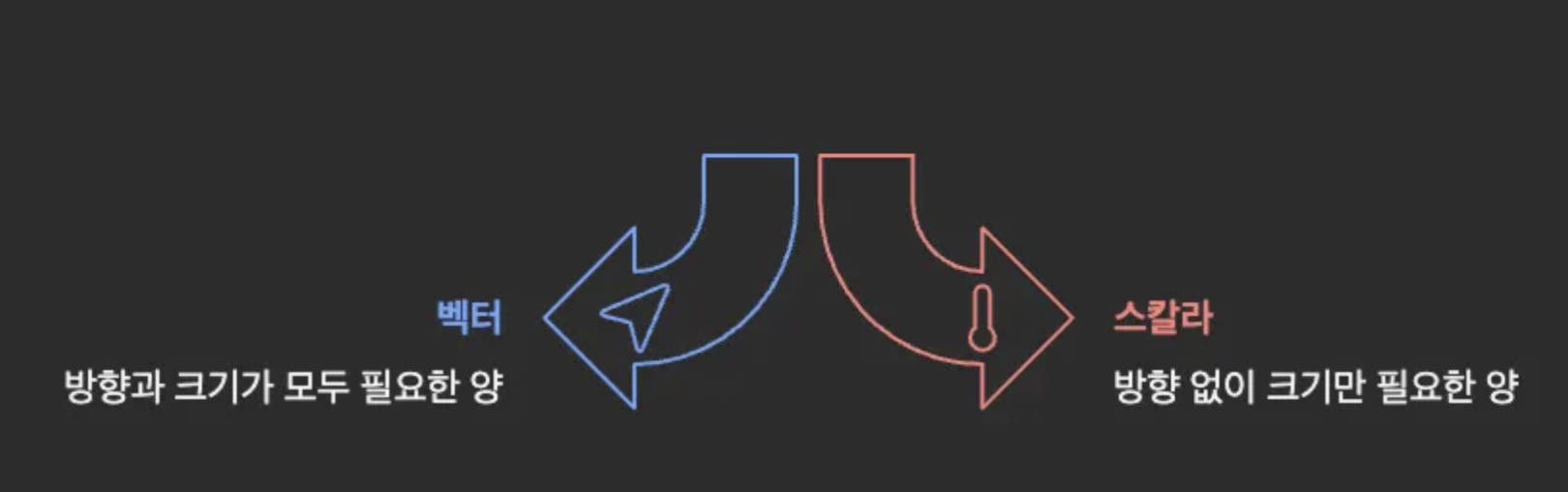
벡터 (Vector)

• 벡터는 방향과 크기를 가진 양이다.
• 반면, 스칼라(Scalar)는 방향 없이 크기만 있는 양이다.
• 예: v = (3, 4) = 오른쪽으로 3, 위로 4만큼의 벡터
• AI/ML에서는 데이터의 특성들을 벡터로 표현한다.

2. 고유값과 고유벡터의 개념

고유값과 고유벡터는 행렬 변환에서 방향은 유지되고 크기만 변하는 특별한 관계를 나타낸다.

• 행렬 A를 선형변환으로 봤을 때, 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌
• 벡터를 고유벡터라 하고 이 상수배 값을 고유값이라 한다.
• 즉, 행렬 변환 후에도 방향은 그대로 유지되고 크기만 몇 배로 변하는 벡터가 고유벡터고, 그 배수가 고유값이다.
• 고유값: 행렬 변환에서 고유벡터가 얼마나 스케일링되는지를 나타내는 스칼라 값 (크기 정보)
• 고유벡터: 행렬 변환 후에도 방향이 바뀌지 않는 특별한 벡터 (방향 정보)
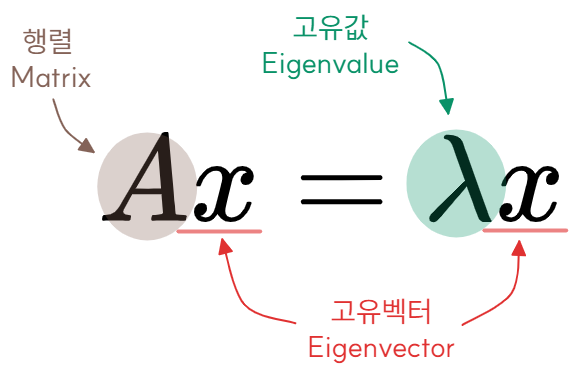
  • A: 행렬
  • v: 고유벡터
  • λ: 고유값 (람다라고 함)

고유값과 고유벡터

위 개념이 중요한 이유는 데이터나 행렬 변환에서 중요한 방향과 그 영향력을 파악할 수 있게 해주며
이런 특성 때문에 고유값 분해, 특이값 분해, 차원 축소 등에 쓰이기 떄문에 중요하다.

3. 고유값 분해 (Eigenvalue Decomposition)

고유값 분해는 정방행렬을 고유값과 고유벡터를 이용해 분해하는 방법이다.

왜 분해하는가?

• 계산이 쉬워짐: 복잡한 행렬 연산을 간단하게
• 데이터 이해: 행렬 안에 숨어있는 주요 패턴 발견
• 차원 축소: 중요한 정보만 골라내기

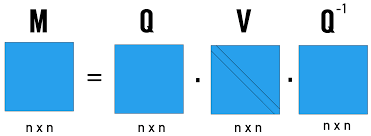
고유값 분해 수식: M = QVQ^(-1)

• M: 원본 정방행렬 (n×n)
• Q: 고유벡터들을 열로 하는 행렬 (n×n)
• V: 고유값들을 대각선에 배치한 대각행렬 (n×n)
• Q^(-1): Q의 역행렬 (n×n)

특이값 분해(Singular Value Decomposition, SVD)

---

1. SVD란?

SVD(특이값 분해)는 임의의 행렬을 세 개의 행렬의 곱으로 분해하는 방법

특이값 분해

고유값 분해 vs SVD 차이점

• 고유값 분해는 정방행렬에 대해서만 가능하지만
• 특이값 분해는 정방행렬뿐만 아니라 행과 열의 크기가 다른 행렬에 대해서도 적용 가능
• 즉, 특이값 분해는 모든 직각 행렬에 대해 가능하다.
  • 고유값 분해: 정방행렬(n×n)에만 적용 가능
  • SVD: 모든 직사각형 행렬(m×n)에 적용 가능

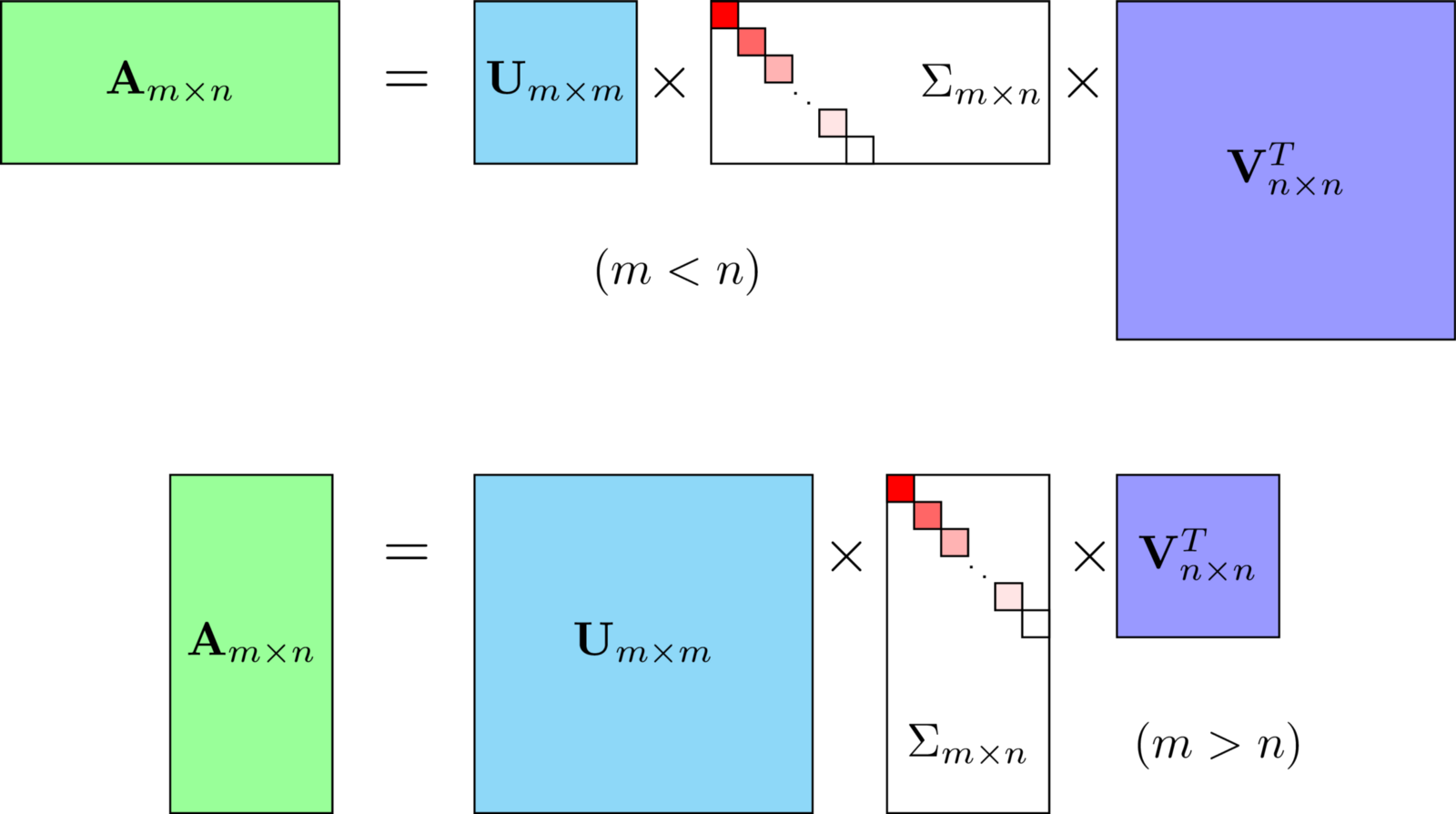
SVD 수식: A = UΣV^T

• U: 왼쪽 특이벡터들 (m×m)
• Σ: 특이값들을 대각선에 배치한 행렬 (m×n)
• V^T: 오른쪽 특이벡터들의 전치 (n×n)

2. 왜 SVD를 사용하는가?

SVD는 데이터의 핵심 정보만 추출하여 계산 효율성과 저장 공간을 획기적으로 개선하는 도구다.

SVD의 핵심 장점

• 차원 축소: 고차원 데이터를 저차원으로 압축하면서 중요한 정보는 보존
• 노이즈 제거: 데이터의 주요 패턴만 남기고 불필요한 정보 제거
• 계산 효율성: 복잡한 행렬 연산을 더 간단하게 처리
• 메모리 절약: 원본보다 훨씬 적은 저장 공간 사용
• 잠재 요인 분석: 데이터 안의 잠재 요인을 파악할 수 있어, 추천, NLP 등 다양한 영역에서 활용 가능

고유값 분해의 한계를 극복

• 고유값 분해: 정방행렬에만 적용 가능 → 실제 데이터는 대부분 직각행렬
• SVD: 모든 형태의 행렬에 적용 가능 → 실무에서 더 유용

AI에서 SVD가 중요한 이유

• 빅데이터 처리: 수백만 차원의 데이터를 몇백 차원으로 압축
• 패턴 발견: 숨겨진 데이터 패턴과 관계 자동 발견
• 추천 정확도 향상: 사용자의 숨겨진 선호도 파악

3. 활용 사례

SVD는 AI 분야에서 차원 축소, 추천 시스템, 자연어 처리 등 다양한 영역에서 활용되고 있다.

주성분 분석 (PCA)

• 목적: 고차원 데이터를 저차원으로 압축하면서 중요한 정보는 유지
• 원리: SVD를 사용해 데이터의 주요 방향(주성분) 찾기
• 활용: 데이터 시각화, 차원의 저주 해결, 노이즈 제거
• 예시: 1000차원 데이터를 2D 그래프로 시각화

추천 시스템

• 목적: 사용자에게 맞춤형 콘텐츠 추천
• 원리: 사용자-아이템 행렬을 SVD로 분해하여 잠재 요인 추출
• 활용: Netflix 영화 추천, Amazon 상품 추천, Spotify 음악 추천
• 장점: 희소한 평점 데이터에서도 패턴 발견 가능

자연어 처리 (NLP)

• 잠재 의미 분석(LSA): 문서-단어 행렬을 SVD로 분해
• 목적: 단어의 숨겨진 의미와 문서 간 유사도 파악
• 활용: 검색 엔진, 문서 분류, 텍스트 요약
• 효과: 동의어나 유사한 의미의 단어들을 자동으로 그룹화

이미지 처리

• 이미지 압축: 중요한 특징만 남기고 용량 줄이기
• 노이즈 제거: SVD로 주요 성분만 복원하여 깨끗한 이미지 생성
• 얼굴 인식: Eigenfaces 기법의 기초 원리