[Upstage AI Lab] 7주차 - ML Advanced

[Upstage AI Lab] 7주차 - Machine Learning 심화 학습 내용

Posted 2025년 05월 09일

By DoorNote

36 min read

[Upstage AI Lab] 7주차 - ML Advanced

들어가며

이번에는 Machine Learning 심화 내용과 전체 파이프라인 및 실습 코드에 대한 내용을 다룰 에정이다.

Data Preprocessing

1. Missing Value Handling

결측치란(Missing Value)? 데이터에서 누락된 관측치 또는 데이터 손실과 더불어 분포를 왜곡시켜 편향을 야기시키는 원인이다.

결측치 표현 종류

N/A (Not Available)
NaN (Not a Number)
NULL 등으로 표현

결측치 매커니즘

완전 무작위 결측

결측치가 다른 변수와 상관 없이 무작위로 발생하는 경우
관측치와 결측치 모두 결측 원인과 독립
센서의 고장, 전산 오류 등의 이유로 발생 가능

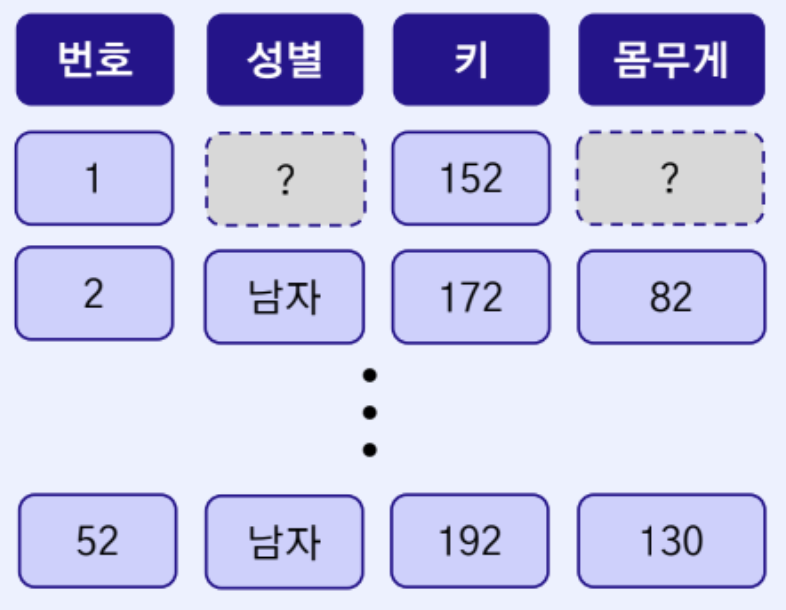
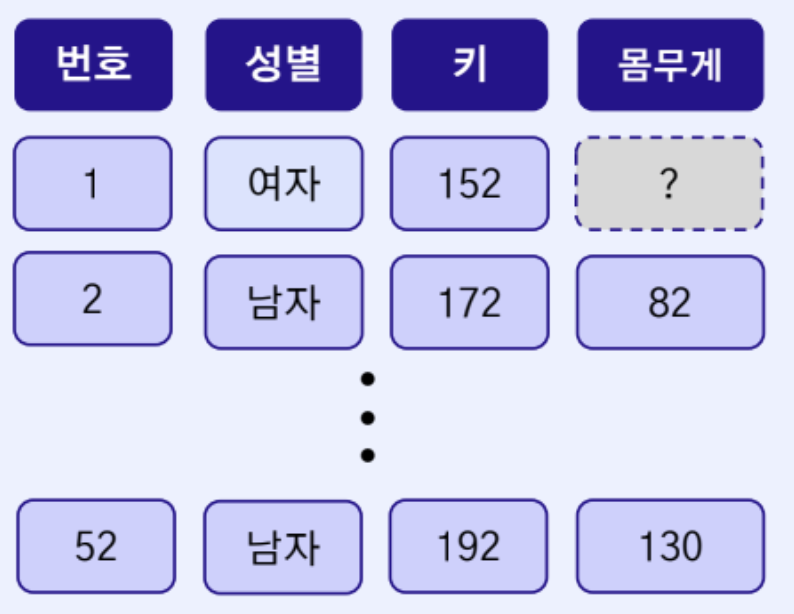
무작위 결측

결측치가 해당 변수와는 무관하나, 다른 변수와 연관되어 있는 경우
다른 변수의 관측치와 연관되어 있기 때문에 예측 모델을 통해 대체 가능
예) 설문조사에서 특정 키에 따라 몸무게에 대한 질문에 무응답인 경우 (몸무게와 키와의 연관)

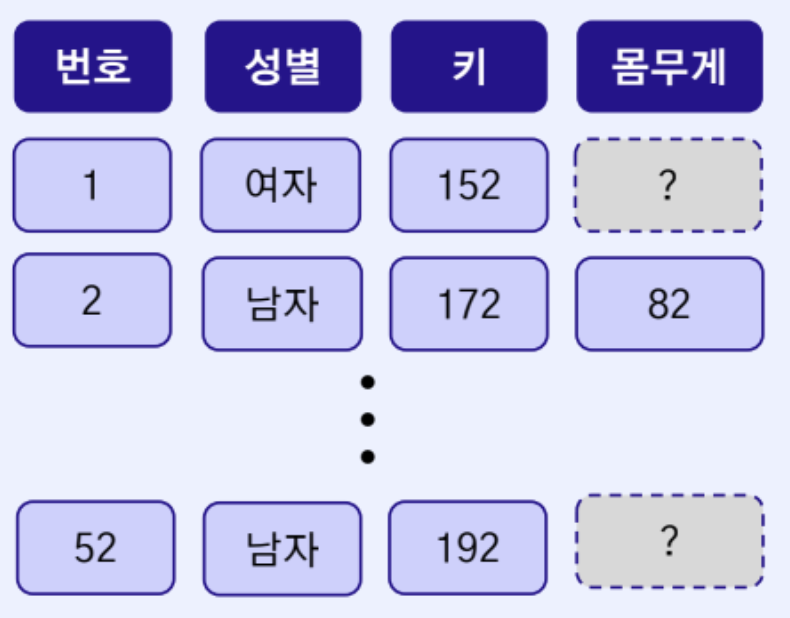
비 무작위 결측

결측의 원인이 해당 변수와 연관되어 발생
MCAR, MCR에 해당되지 않는 결측 유형
예) 신체 정보 관련 설문조사에서 몸무게가 비교적 높은 응답군에서 결측이 많이 발생

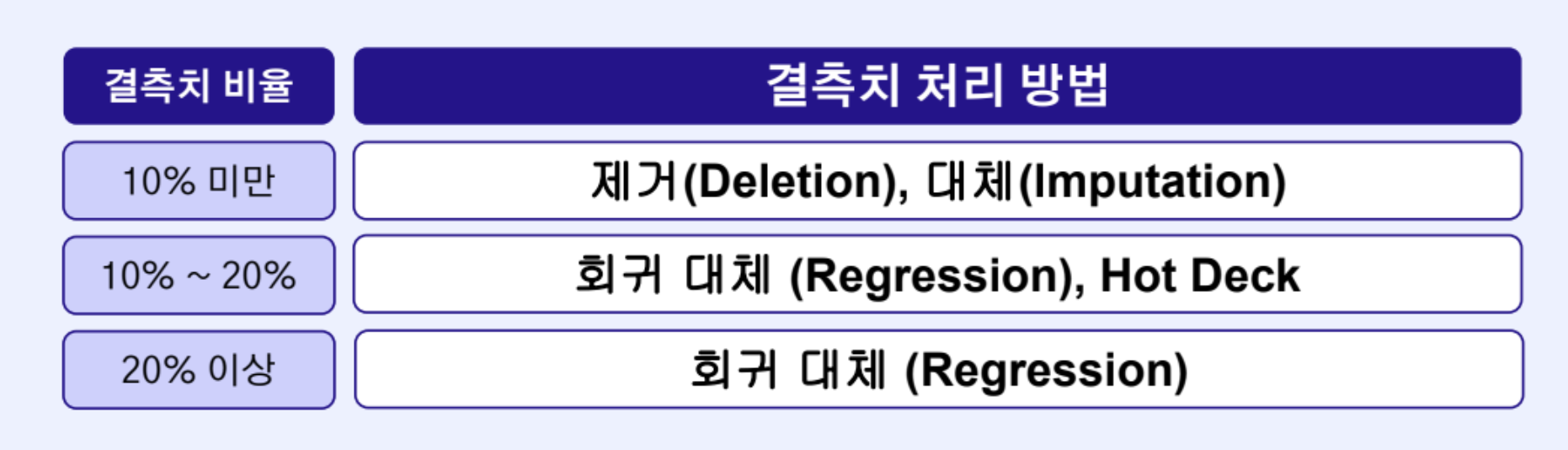
결측치 삭제

장점
- 결측치를 처리하기 편리
- 결측치가 데이터 왜곡의 원인이라면, 삭제로 인한 왜곡 방지와 알고리즘 모델 성능 향상 기대
단점
- 결측치에도 데이터 특성이 유효한 경우가 존재
- 삭제된 데이터로 인하여 남은 데이터에 편향이 만들어질 가능성
- 관측치의 정보가 줄어들게 되므로 알고리즘 모델에 악영향

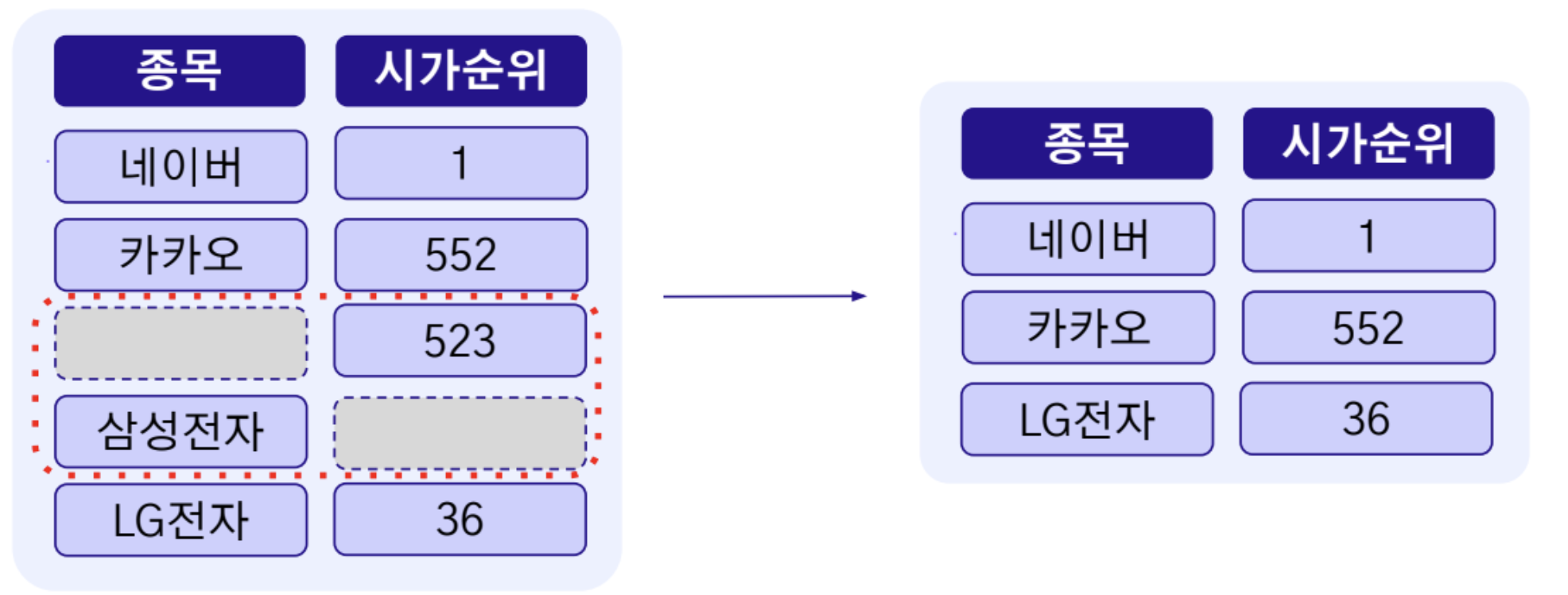
목록 삭제

변수에 결측치가 존재하는 해당 행을(Row) 제거
모든 변수가 결측치 없이 채워진 형태의 행만 분석 및 모델링에 활용하는 방식

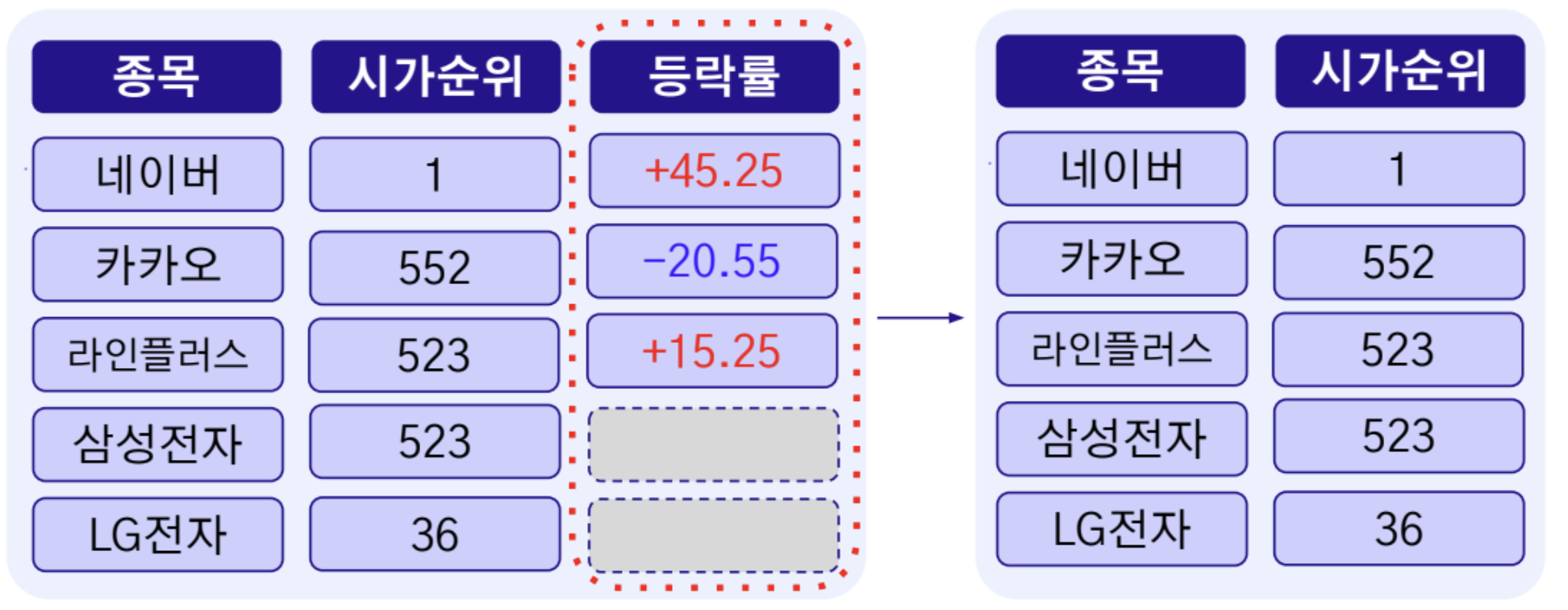
열 삭제

변수에 결측치가 존재하는 해당 열을(Column) 제거

결측치 대체

장점
- 대체된 값은 데이터의 통계 특성을 반영하므로 정보를 안정적으로 보존 가능
- 데이터의 샘플이 그대로 유지되기 때문에 알고리즘 모델에 원본 크기로 적용 가능
단점
- 통계값으로 인해 변수의 분산이 감소하여 변수간 상관관계가 낮아지는 문제 발생
종류
- 결측치를 관측치의 통계값(평균값, 최빈값, 중앙값)으로 대체
- 회귀 대체: 변수간의 관계를 파악 후, 모델로 예측하여 결측치를 대체하는 방식

2. Outlier

이상치란(Outlier)? 변수의 분포상 비정상적으로 극단적이며, 일반적인 데이터 패턴을 벗어나는 관측치

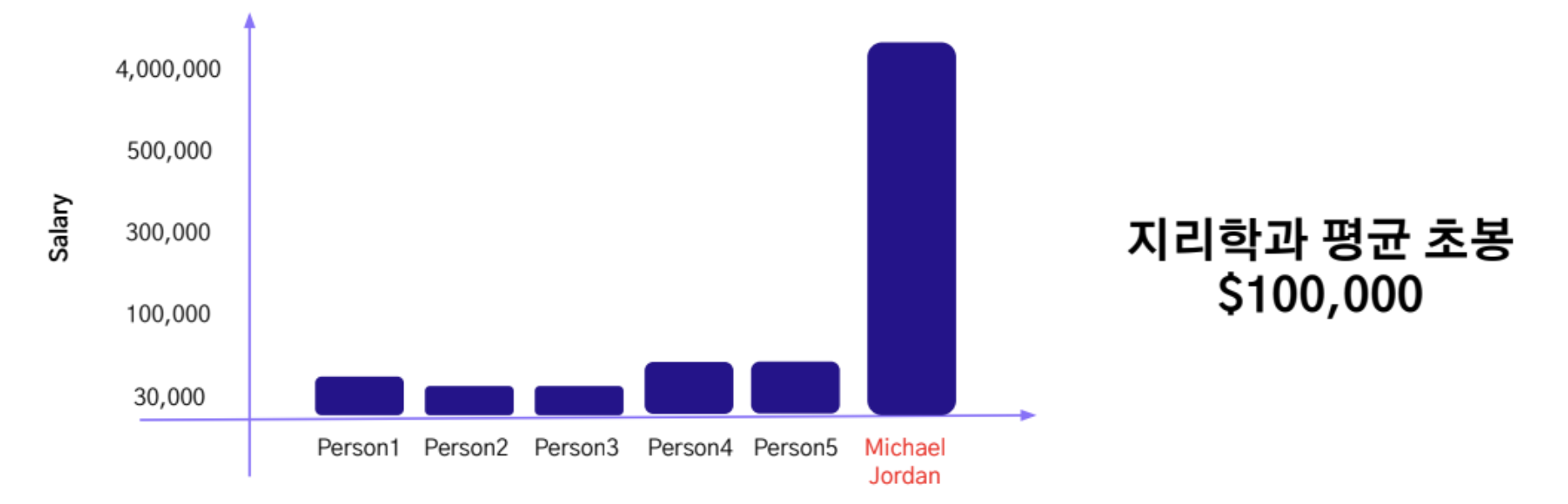
평균값과 같은 통계적 중요 결과를 왜곡 시키는 원인
예) 노스캐롤라이나 대학교 지리학과의 평균 초봉은 모든 과를 통틀어 가장 높은 수치를 한때 기록 이는 당시 슈퍼스타였던 마이클조던이 노스캐롤라이나 대학교 지리학과를 졸업했기 때문

이상치 탐지 및 제거가 필요한 이유

데이터 분석 및 탐색 시에 패턴과 인사이트를 도출하는 것이 가능
데이터로부터 도출된 명확한 패턴과 인사이트는 올바른 의사결정에 도움
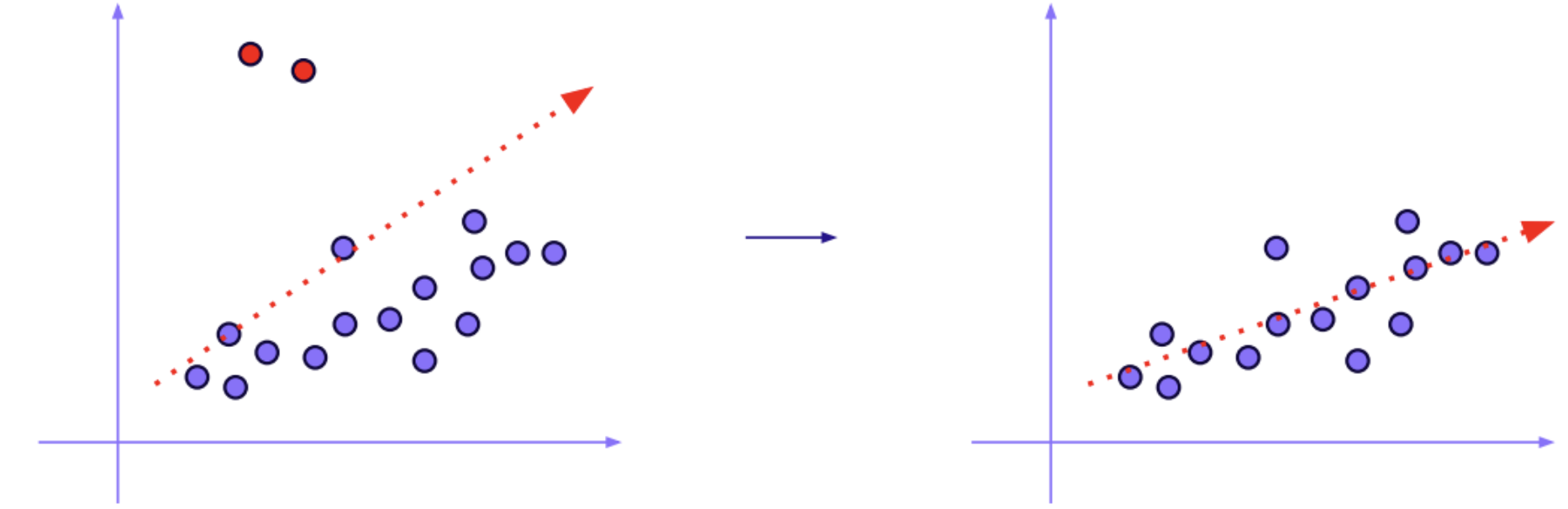
데이터 전체를 왜곡시키는 이상치를 제거하여 모델의 안정성 향상을 기대
대표적으로 회귀분석은 이상치에 민감 (아래 그림)

이상치 종류

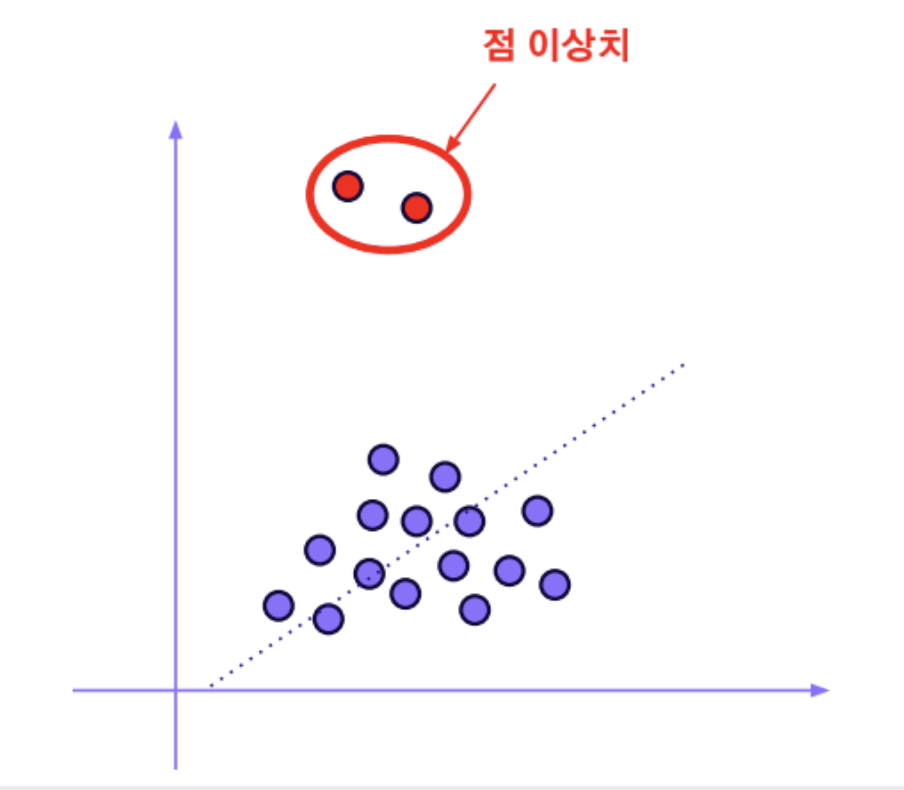
점 이상치

대부분의 관측치들과 동떨어진 형태의 이상치
변수의 분포상 비정상적인 패턴을 가졌기 때문에 탐지가 어렵지 않은 케이스

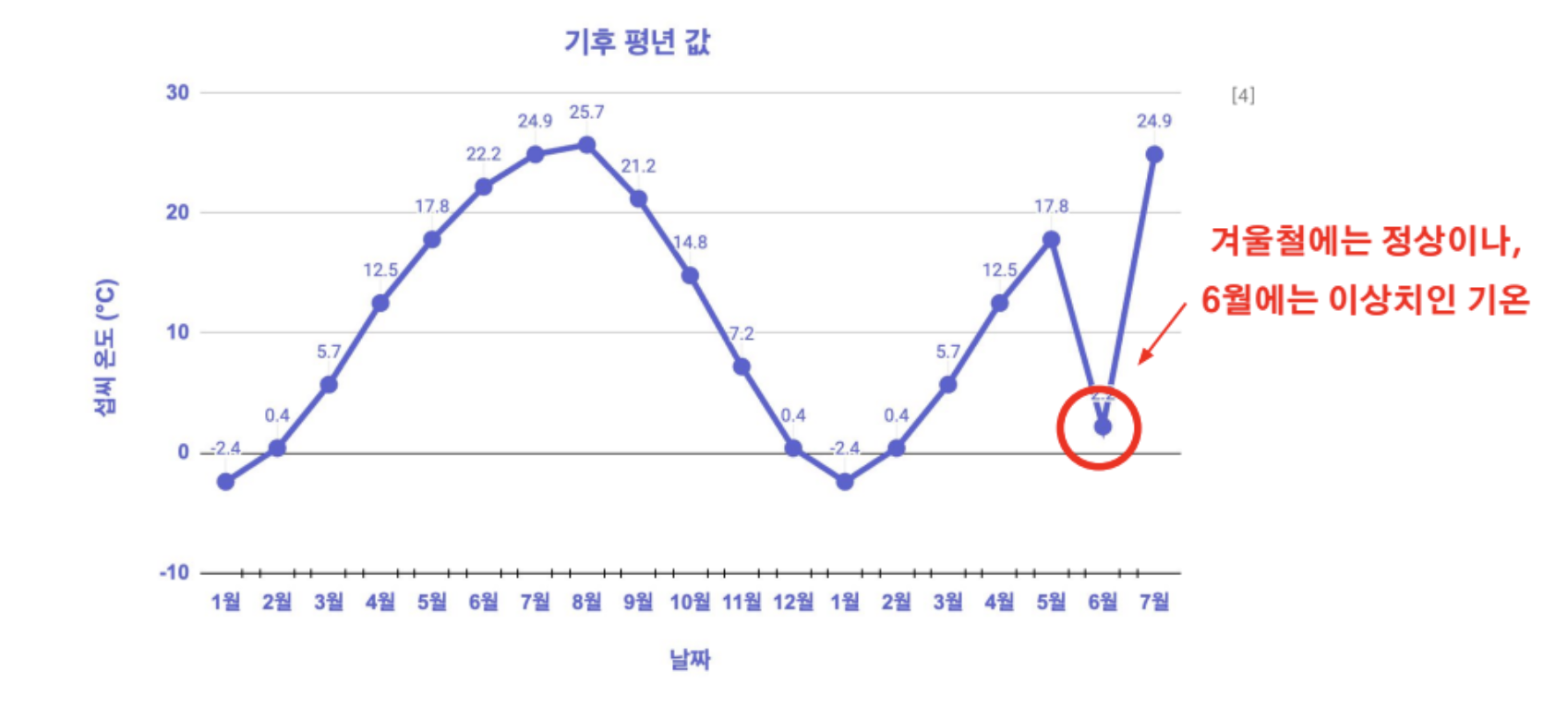
상황적 이상치

정상적인 데이터 패턴이라도 상황에 따라 이상치로 변환되는 형태
상황은 주로 시점에 따라 바뀌기 때문에 시계열 데이터에서 주로 나타나는 케이스

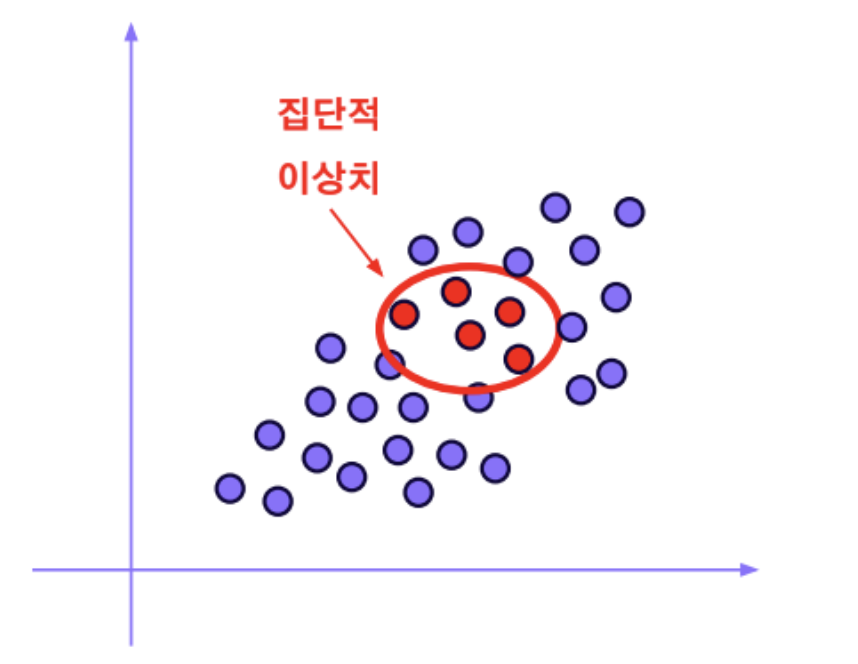
집단적 이상치

데이터 분포에서 집단적으로 편차가 이탈되어 이상치로 간주
관측치 개별로 보았을 때는 이상치처럼 보이지 않는 것이 특징
예) 스팸 메일은 일반 메일과 형태가 유사하지만, 정상적이지 못한 메일

이상치 탐지

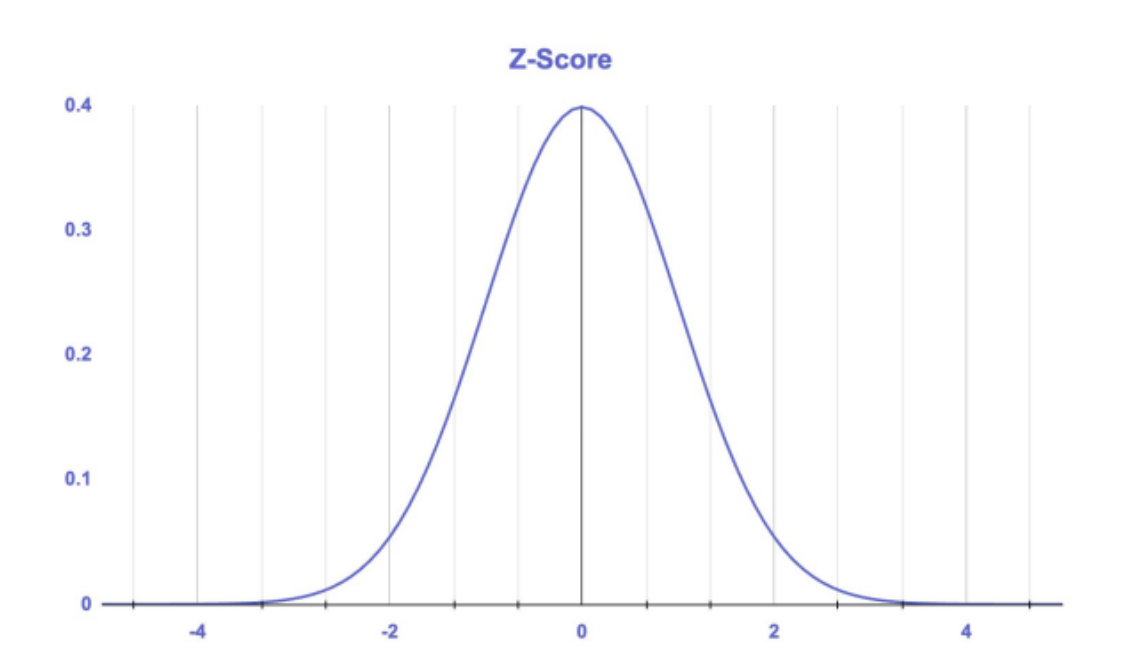
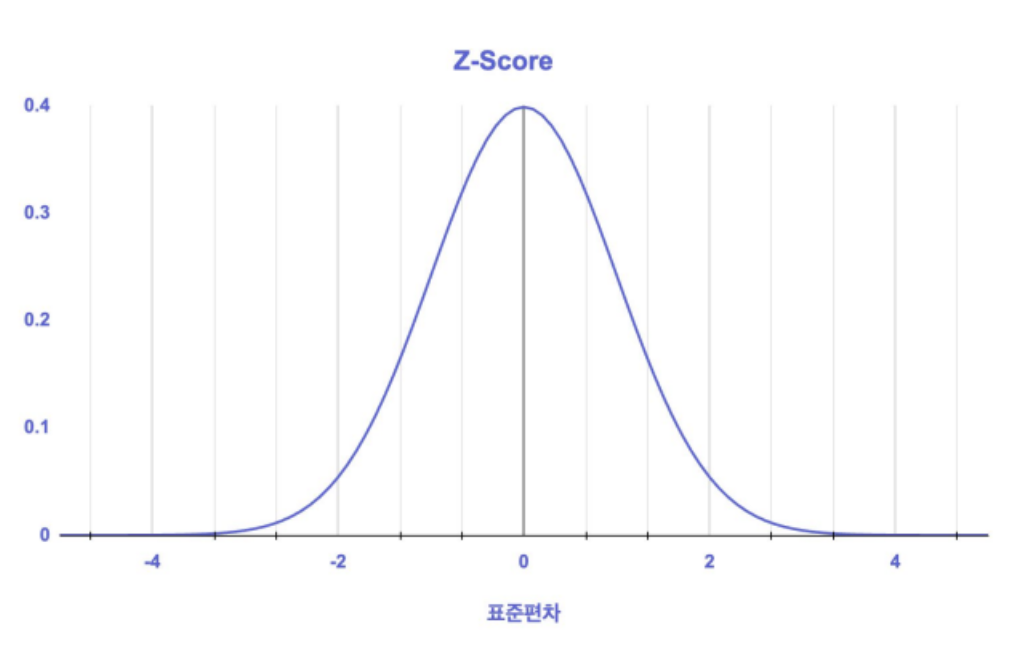
Z-Score

평균으로부터의 표준편차 거리 단위를 측정하여 이상치를 탐지하는 방법
Z 값을 측정하여 이상치를 탐색
Z 값이 2.5~3정도 수치가 나오면 이상치로 판별
데이터가 정규분포를 따른다고 가정
장점
- 데이터에서 이상치를 간단하게 탐지 가능
단점
- 표준화된 점수를 도출하는 과정이기 때문에 데이터가 정규분포를 따르지 않는 경우 효과적이지 않을 가능성
- Z-Score를 구성하는 평균과 표준편차 자체가 이상치에 민감 (Modified Z-Score를 이용하는 방법도 존재)

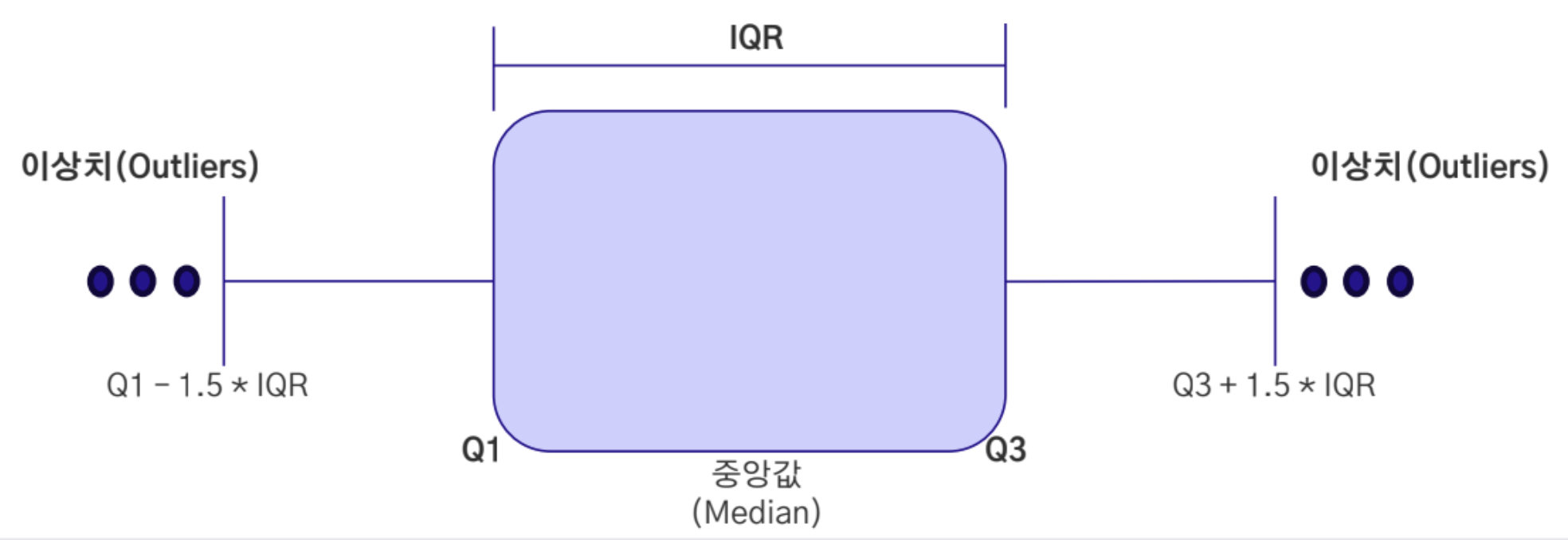
IQR

IQR은 상위 75%와 하위 25% 사이의 범위
IQR은 Q3(제 3사분위)에서 Q1(제 1사분위)를 뺀 위치
Q1 - 1.5 * IQR 및 Q3 + 1.5 * IQR 을 최극단의 이상치로 판단하여 처리
장점
- 데이터의 중앙값과 분포만을 통해 이상치를 식별하므로 직관적
- 표준편차 대신 백분위수(25%, 75%)를 사용하므로 이상치에 강건한 특징
- 데이터가 몰려 있는 경우라도 분포를 활용하기 때문에 효과적
단점
- 이상치의 식별 기준이 백분위수에 의존
- 왜도가 심하거나 정규분포를 따르지 않는 경우 제대로 작동하지 않을 가능성

이상치 처리

삭제

이상치에 해당하는 데이터 포인트(값, 인스턴스)를 제거하는 방법
다만, 이상치는 중요한 정보를 내포하고 있는 경우도 존재
이상치는 도메인 지식에 기반하여 객관적인 상황에 맞게 제거하는 것이 필요

대체

통계치(평균, 중앙, 최빈)으로 이상치를 대체
상한값(Upper boundary), 하한값(Lower boundary) 정해놓고 이상치가 경계를 넘어갈 때 대체
회귀 및 KNN 등의 거리기반 알고리즘 등을 이용해 이상치를 예측 및 대체하는 방식도 존재

변환(Transformation)

변수 내에서 이상치를 완화시킬 수 있는 방법

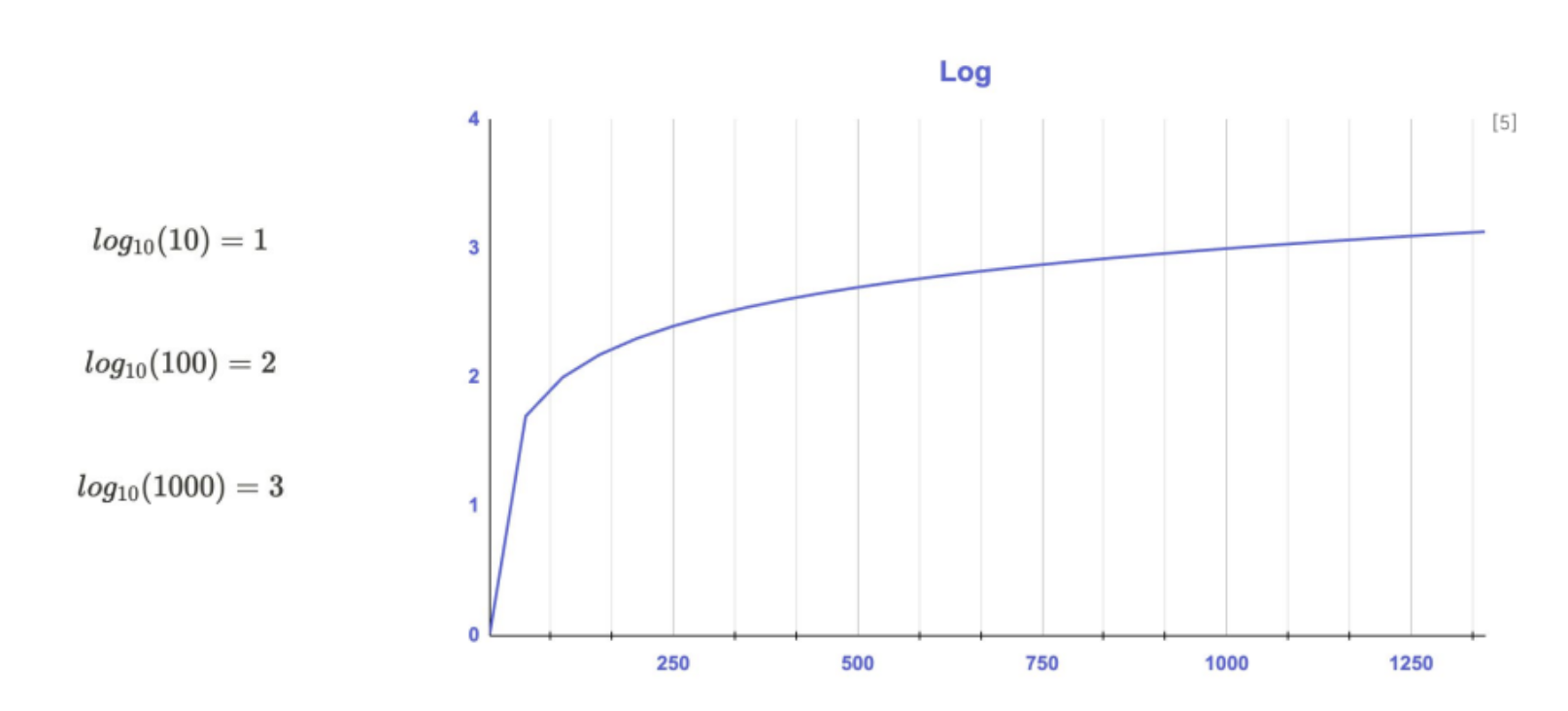
로그 변환 (Log Transformation)

양의 왜도 완화에 효과적
크기가 큰 값을 줄이는 데 효과적이며, 오른쪽 꼬리가 긴 분포 완화에 적합
0 이하 값은 log(x + 1) 형태로 처리

  
import numpy as np
df['log_col'] = np.log1p(df['original_col'])  # log(x + 1)

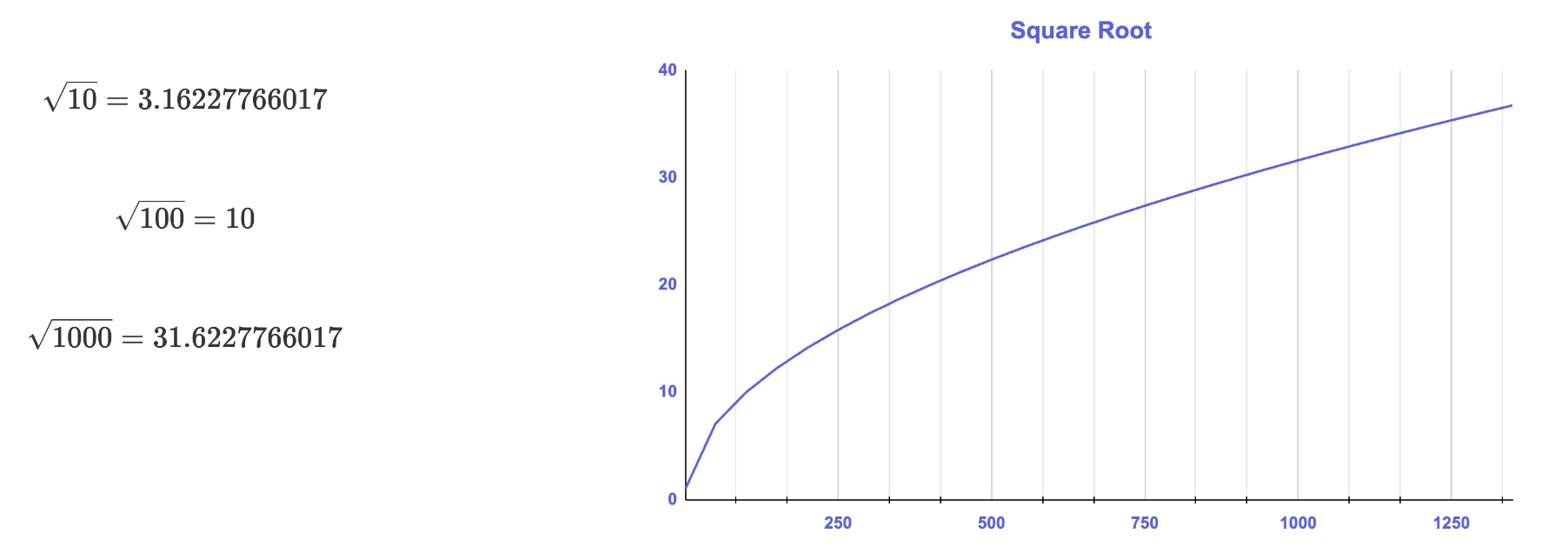
제곱근 변환 (Square Root Transformation)

0 이상이며, 약한 양의 왜도를 가진 변수
로그보다 완만하게 값을 축소함
데이터 분포가 오른쪽으로 치우쳐 있으나 극단적이지 않을 때 적합
0 이상인 값에만 적용 가능

  
df['sqrt_transformed'] = np.sqrt(df['original_col'])

Box-Cox 변환 (Box-Cox Transformation)

값이 모두 양수여야 함 (0 이하 불가)
연속형 변수에만 적용
정규성 확보에 유리
로그/제곱근/역수 등을 포함한 람다 기반 일반화 방식
선형 회귀, ANOVA 등 정규성 가정을 전제로 한 모델에 적합

  
from scipy.stats import boxcox
df['boxcox_transformed'], _ = boxcox(df['original_col'])  # 반드시 양수

3. Scaling

스케일링이란(Scaling)? 변수마다 다른 값의 범위(Scale)를 통일시켜 모델이 특정 변수의 크기 차이로 인해 편향되지 않도록 조정하는 전처리 과정

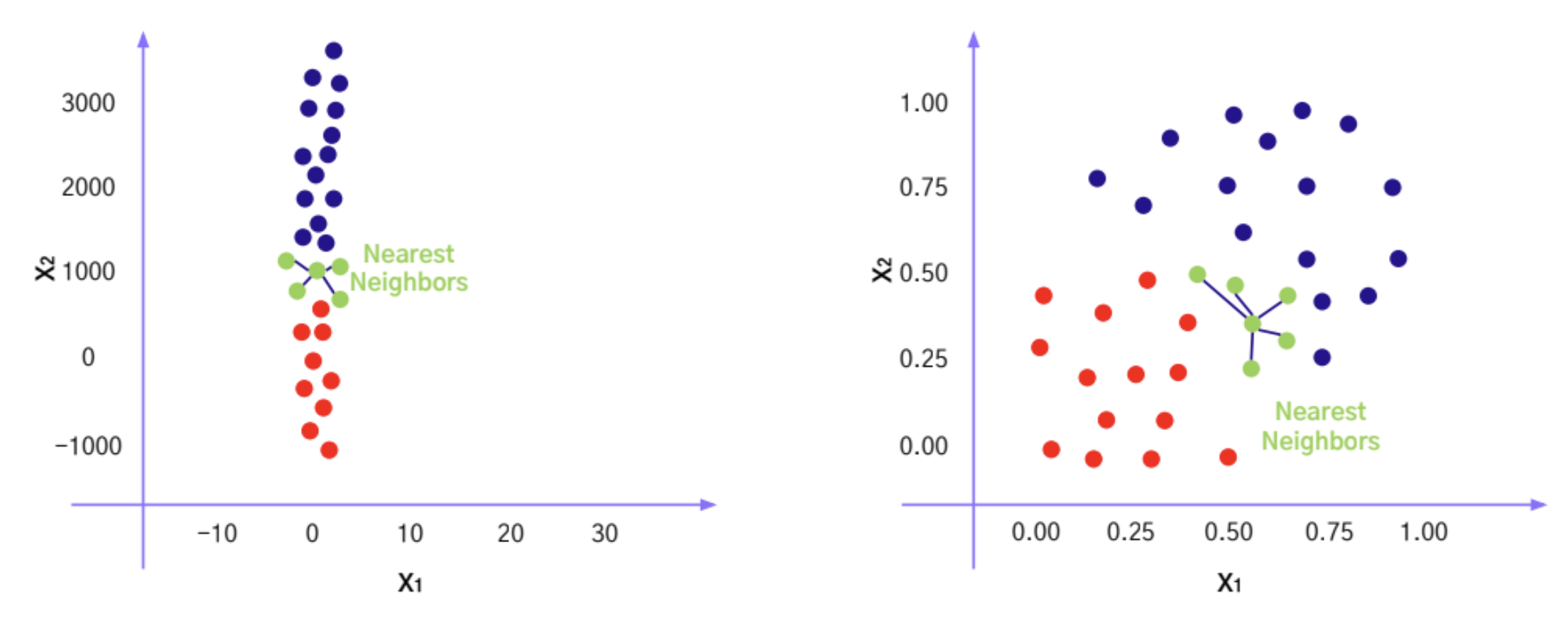
Scaling 필요 이유

수치형 독립 변수들의 수치 범위가 다르게 존재하면 종속 변수에 각기 다르게 영향을 미친다.
수치 범위가 큰 변수일수록 다른 변수에 비해 더 중요하게 인식될 수 있음
변수들이 동일한 범위로 스케일링이 되어 있지 않다면, 결과가 올바르지 않은 리스크 존재
독립 변수들의 영향력을 동등하게 변환시켜 KNN과 같은 거리기반 알고리즘에 효과
KNN은 벡터간 거리(유클리드&맨하튼 거리법)를 측정하여 데이터를 분류하는 방식

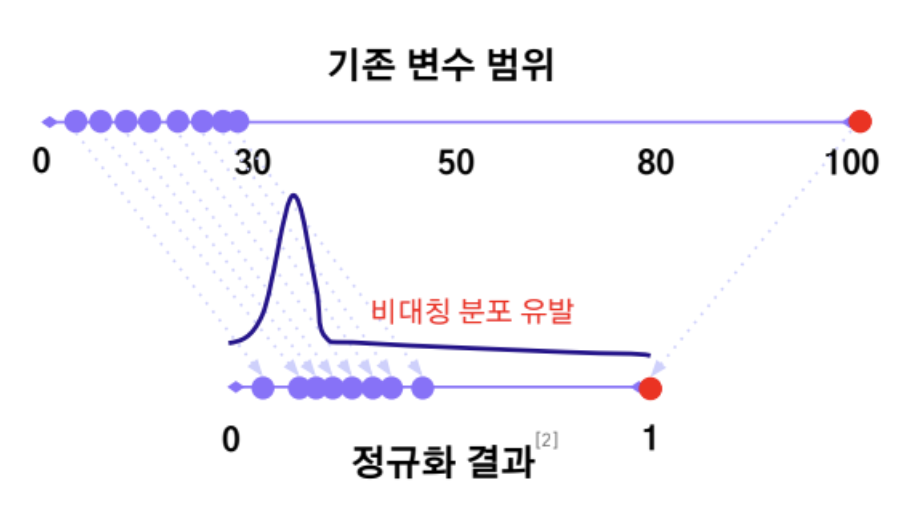
Min-Max Scaling

각 변수의 값을 최솟값과 최댓값 기준으로 선형 변환
전체 데이터 기준이므로, 학습/테스트 분리 후에는 학습셋 기준으로 변환해야 함
이상치에 매우 민감
- 최댓값이나 최솟값이 이상치라면 전체 스케일이 왜곡됨

\[X' = \frac{X - X_{\text{min}}}{X_{\text{max}} - X_{\text{min}}}\]

$X$: 원본 값
$X’$: 스케일링된 값
$X_{\text{min}}, X_{\text{max}}$: 해당 컬럼의 최솟값, 최댓값

  
from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler() # 기본값은 0~1
df[['scaled_col']] = scaler.fit_transform(df[['original_col']])

Standard Scaling

변수의 수치 범위(스케일)를 평균이 0, 표준편차가 1이 되도록 변경(Z-score)
평균과의 거리를 표준편차로 나누기(정규분포의 표준화 과정)
즉, 평균에 가까워질수록 0으로, 평균에서 멀어질수록 큰 값으로 변환

\[X' = \frac{X - \mu}{\sigma}\]

$X$: 원본 값
$X’$: 스케일링된 값
$\mu$: 평균
$\sigma$: 표준편차

  
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
df[['scaled_col']] = scaler.fit_transform(df[['original_col']])

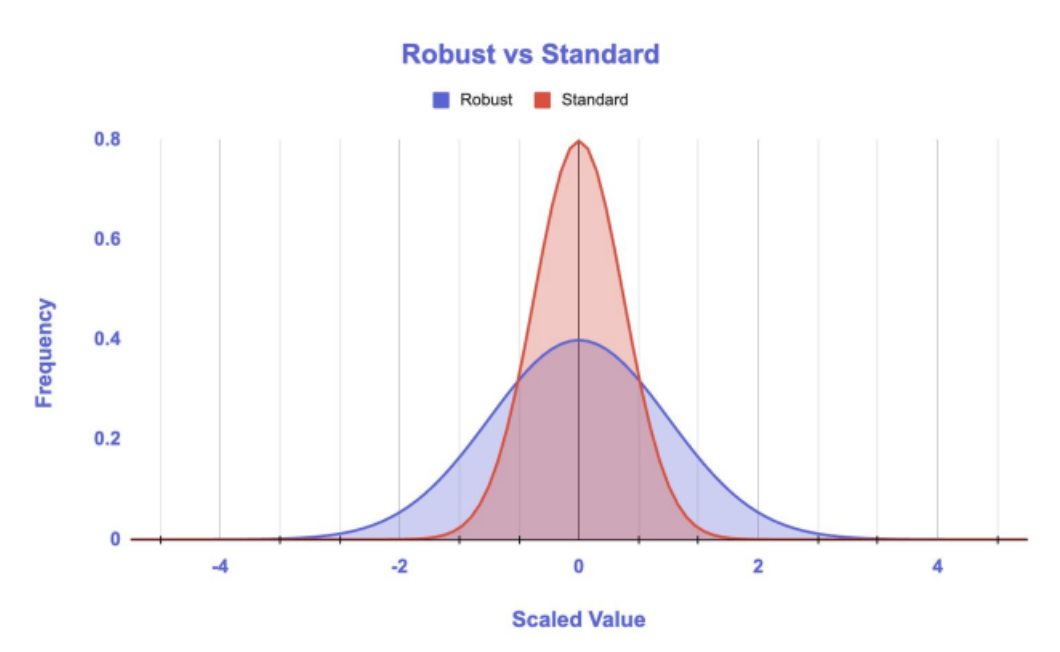
Robust Scaling

중앙값(median)과 IQR(사분위 범위)를 기준으로 스케일링
이상치의 영향을 최소화하여 스케일을 조정하는 방식
이상치(outlier)에 매우 강건(robust)
데이터가 정규분포와 유사하지 않아도 효과적
값의 상대적 위치를 유지하면서 스케일링

\[X' = \frac{X - Q_2}{Q_3 - Q_1}\]

$X$: 원본 값
$X’$: 스케일링된 값
$Q_1$, $Q_3$: 1사분위수, 3사분위수
$Q_2$: 중앙값 (Median)
$Q_3 - Q_1$: IQR (Interquartile Range, 사분위 범위)

  
from sklearn.preprocessing import RobustScaler

scaler = RobustScaler()
df[['scaled_col']] = scaler.fit_transform(df[['original_col']])

4. Encoding

Encoding이란? 모델이 문자형 데이터(범주형 변수)를 이해할 수 있도록, 수치형으로 변환하는 전처리 과정
특히 범주형 변수는 그대로 사용할 수 없기 때문에 적절한 인코딩 방식 선택이 중요하다.

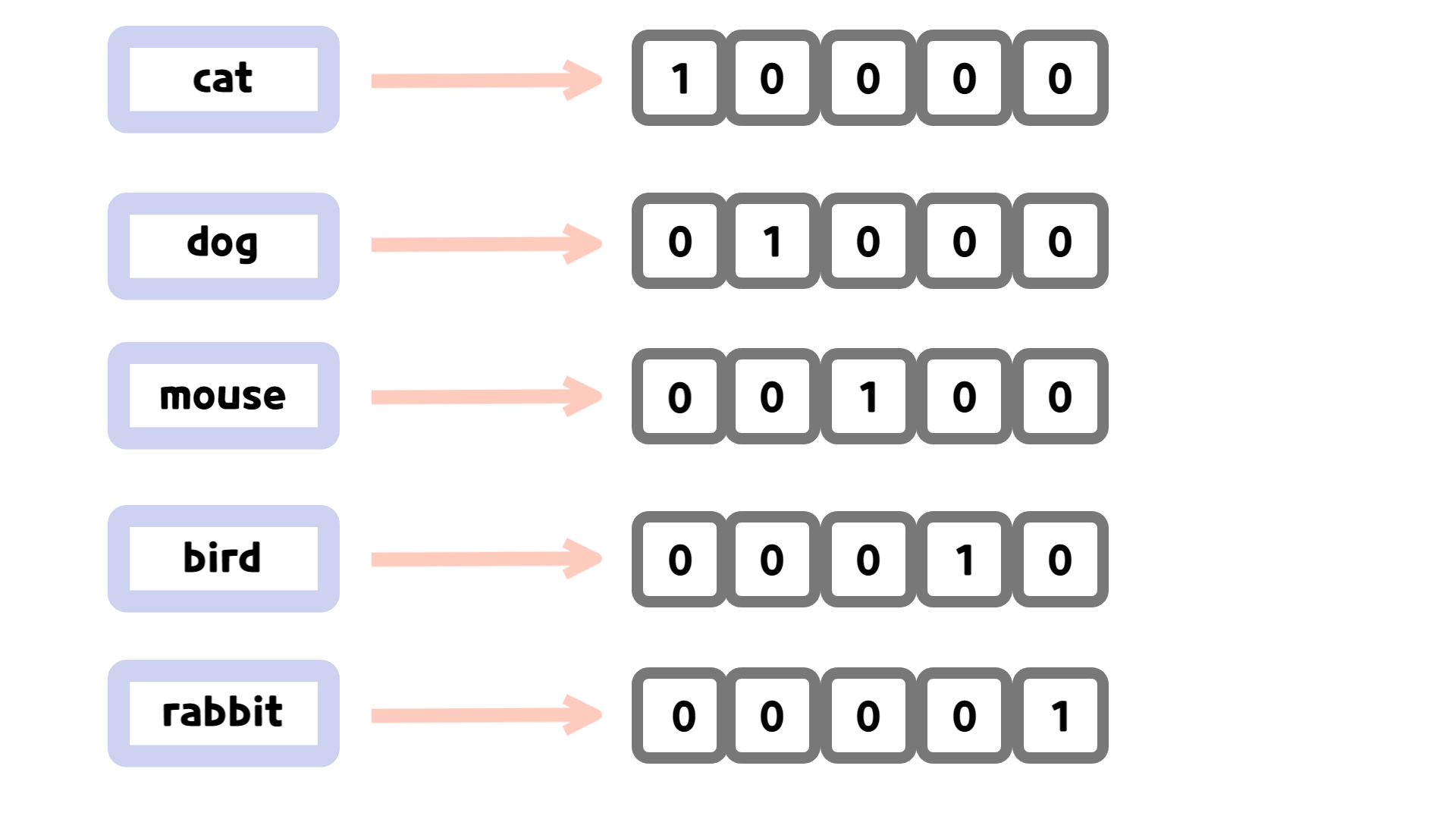
One-Hot Encoding

범주 변수를 0과 1로만 구성된 이진(binary) 벡터 형태로 변환하는 방법
고유 범주 변수 크기와 동일한 이진 벡터를 생성
범주에 해당하는 값만 1 설정, 나머지는 모두 0 변환
장점
- 변수의 이진화를 통해 컴퓨터가 인식하는 것에 적합
- 알고리즘 모델이 변수의 의미를 정확하게 파악 가능
단점
- 고유 범주 변수의 크기가 늘어날 때마다 희소 벡터 차원이 늘어나는 문제점이 존재
- 벡터의 차원이 늘어나면 메모리 및 연산에 악영향
- 차원의 저주 발생

  
import pandas as pd
from sklearn.preprocessing import OneHotEncoder

# pandas의 get_dummies 사용
df = pd.DataFrame({'Color': ['Red', 'Green', 'Blue', 'Green', 'Red']})
df_encoded = pd.get_dummies(df, columns=['Color'])

# Scikit-learn의 OneHotEncoder 사용
encoder = OneHotEncoder(sparse=False)  # sparse=True일 경우 희소 행렬로 반환됨
encoded_array = encoder.fit_transform(df[['Color']]) # 학습 및 변환
encoded_df = pd.DataFrame(encoded_array, columns=encoder.get_feature_names_out(['Color']))

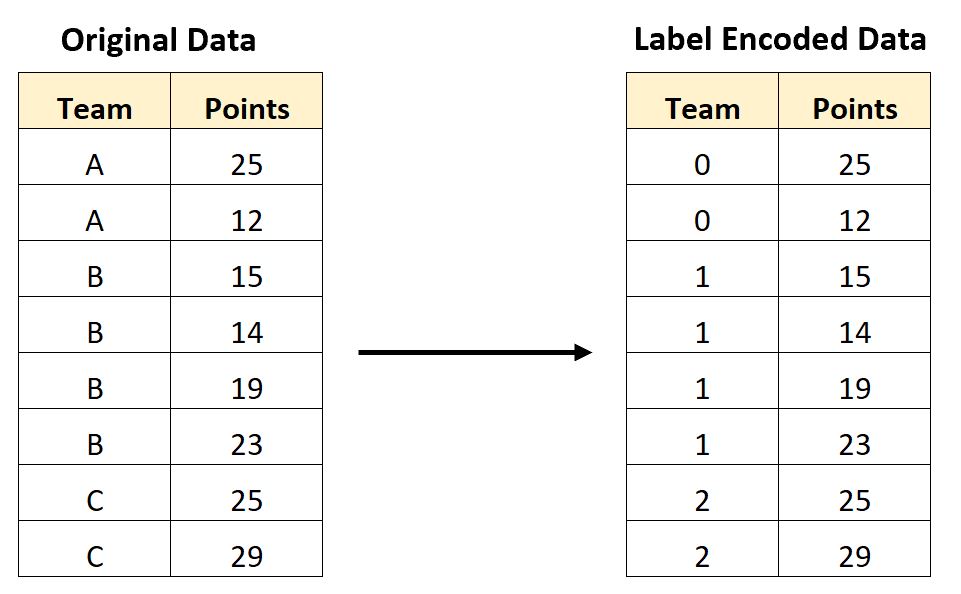
Label Encoding

이진 벡터로 표현하는 원-핫 인코딩과 다르게 각 범주를 정수로 표현
하나의 변수(컬럼)으로 모든 범주 표현 가능
순서가 존재하는 변수들에 적용할 경우 효율적
장점
- 범주 당 정수로 간단하게 변환 가능
- 하나의 변수로 표현 가능하기 때문에 메모리 관리 측면에서 효율적
단점
- 순서가 아닌 값을 순서로 인식할 수도 있는 문제가 발생

  
import pandas as pd
from sklearn.preprocessing import LabelEncoder

le = LabelEncoder() # LabelEncoder 객체 생성
df['Color_encoded'] = le.fit_transform(df['Color']) # 레이블 인코딩 수행

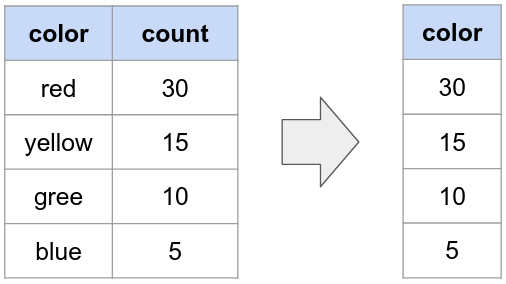
Frequency Encoding

고유 범주의 빈도 값을 인코딩
빈도가 높을수록 높은 정숫값을, 빈도가 낮을수록 낮은 정숫값을 부여 받는 형태
빈도 정보가 유지되어 학습에 적용시킬 수 있는 것이 특징
Count Encoding이라고도 불림
장점
- 빈도라는 수치적인 의미를 변수에 부여 가능
- 하나의 변수(컬럼)로 표현 가능하기 때문에 메모리 관리 측면에서 효율적
단점
- 다른 특성의 의미를 지니고 있어도 빈도가 같으면, 다른 범주간 의미가 동일하게 인식될 가능성이 존재

  
import pandas as pd
import category_encoders as ce

# pandas로 직접 구현
freq_map = df['Color'].value_counts(normalize=False)  # normalize=True → 비율로 반환
df['Color_encoded'] = df['Color'].map(freq_map) # 매핑하여 인코딩 컬럼 생성

# category_encoders 사용
encoder = ce.CountEncoder(normalize=True) # FrequencyEncoder 생성
df_encoded = encoder.fit_transform(df) # 적용

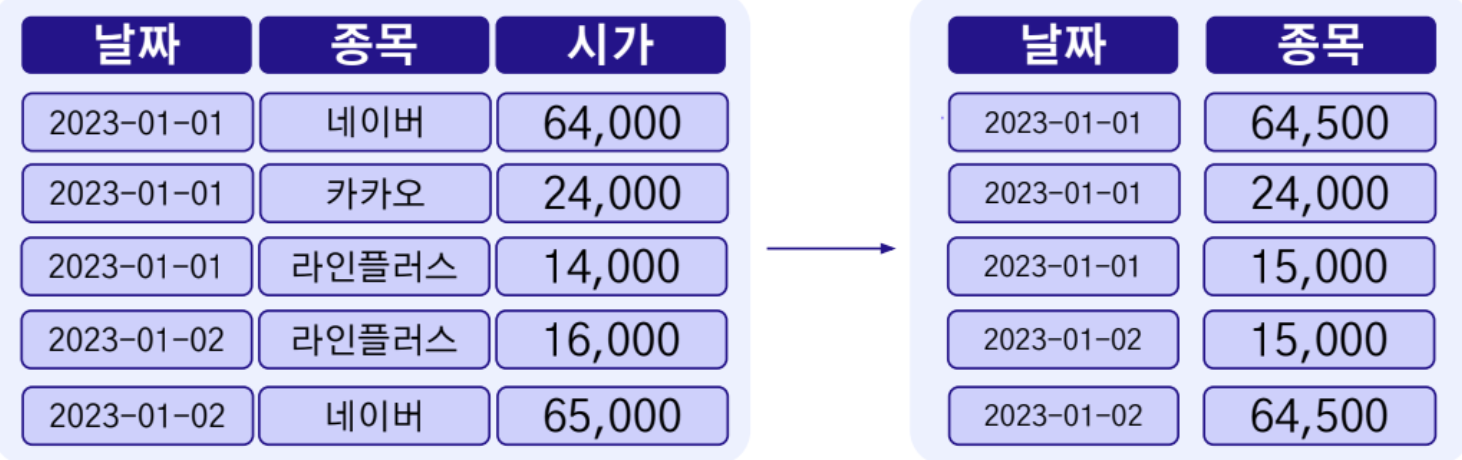
Target Encoding

특정(타겟) 변수를 통계량(평균)으로 인코딩하는 방식
범주형 변수가 연속(Continuous)적인 특성을 가진 값으로 변환
범주형 변수가 특정 타겟 변수와 어떤 관련성이 있는지 파악하기 위한 목적도 존재
Mean Encoding이라고도 불림

장점
- 범주 간 수치적인 의미를 변수에 부여 가능
- 타겟 변수라는 추가적인 정보를 가진 변수에 의존하므로 추가된 정보를 알고리즘에 입력 가능
- 하나의 변수로 표현 가능하기 때문에 메모리 관리 측면에서 효율적
단점
- 타겟 변수에 이상치가 존재하거나, 타겟 변수의 범주 종류가 소수라면 과적합 가능성이 존재
- 데이터를 분할했을 때, 타겟 변수 특성이 학습 데이터에서 이미 노출되었기 때문에 데이터 유추 발생

  
import pandas as pd
import category_encoders as ce

# pandas로 직접 구현
target_mean = df.groupby('Color')['Price'].mean() # 범주별 평균 타겟값 계산
df['Color_encoded'] = df['Color'].map(target_mean) # 매핑하여 새로운 인코딩 컬럼 생성

# category_encoders 사용
encoder = ce.TargetEncoder(cols=['Color']) # TargetEncoder 객체 생성
df['Color_encoded'] = encoder.fit_transform(df['Color'], df['Price']) # 적용

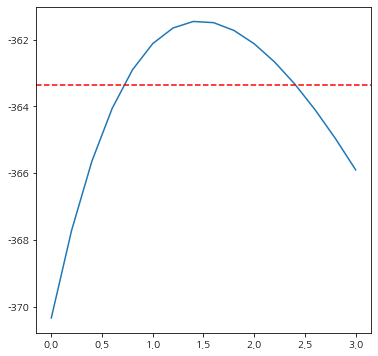
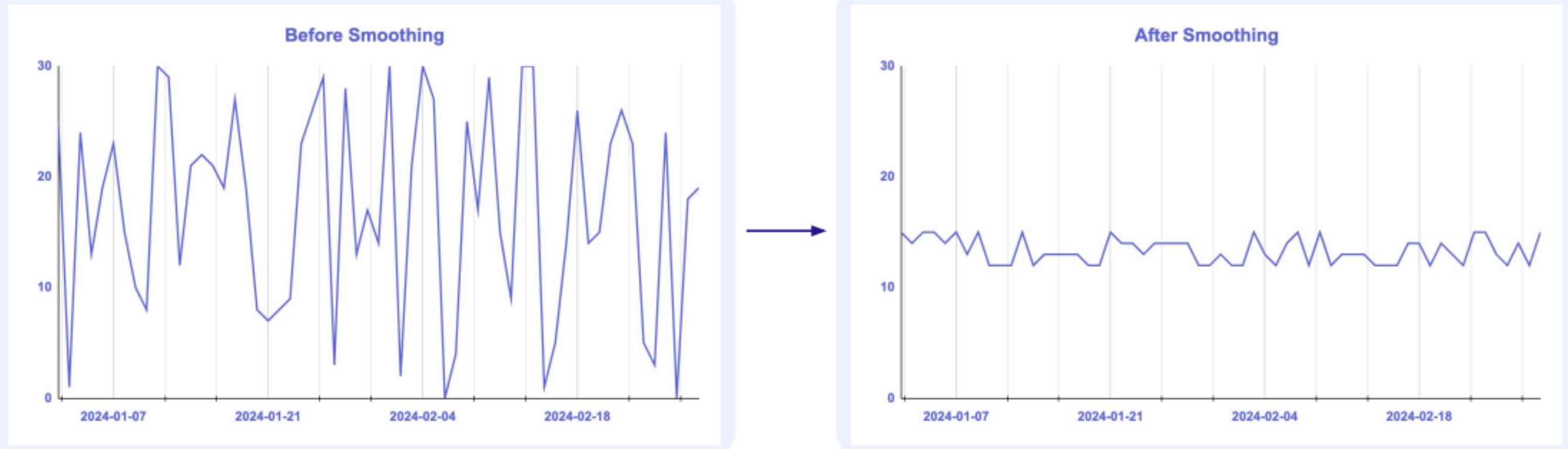
타겟 인코딩의 과적합 방지

스무딩(Smoothing)

전체(학습 + 검증) 데이터셋의 평균에 가깝게 전환
위 그림처럼 기존 관측치를 전체 평균에 가까워지도록 규제를 가하는 방법

K-Fold (교차 검증)

데이터 샘플 내에서도 다시 여러 데이터 샘플(Fold)로 재구성하여 각각 샘플을 타겟 인코딩을 하는 방식
타겟 인코딩 값이 보다 다양하게 생성

5. Feature Selection

Feature selection 이란? 학습에 필요한 변수를 중요도에 따라 선택하는 과정

변수 선택을 진행하는 이유

차원의 저주 : 데이터의 차원이 학습 데이터 수보다 증가하면서 모델의 성능이 저하되는 현상
차원의 저주 해소 : 모델의 복잡도를 낮출 수 있음
모델의 성능 향상 및 과적합(Overfitting) 완화
학습 및 추론시간, 메모리 개선
더 적은 변수들을 활용해 해석 가능성 증대

Filter methods

변수간의 통계적 관계를 평가해 변수의 중요도를 결정하는 방법

통계적 관계 = 변수 간의 상관관계, 분산 고려
상관관계 : 변수들 간의 상관계수를 계산해, 상관관계가 높은 변수들을 제거
분산 : 분산이 낮은 변수들을 제거해 변동성이 낮은 변수 제거

Wrapper methods

실제 모델의 성능을 활용하여 변수를 선택하는 방법

모델을 반복적으로 학습시키고 검증하는 과정에서 최적의 변수 조합을 찾는 방법
순차적 특성 선택(Sequential Feature Selection) : 변수를 하나씩 추가하면서 탐색
재귀적 특성 제거(Recursive Feature Elimination) : 변수를 하나씩 제거하면서 탐색

Embedded methods

모델의 훈련 과정에서 변수의 중요도를 평가해, 이를 기반으로 모델에 대한 변수의 기여도를 결정하는 방법

트리 모델 Feature importance 기반 : 트리 split 기여도에 따른 importance를 이용
규제(Regularizer) 기반 : L1, L2 등의 규제를 이용해 변수의 기여도 결정
모델의 특성을 잘 반영하고, 변수의 중요도와 모델의 복잡성을 동시에 고려 가능

Model Selection

1. Linear Regression

선형 회귀(Linear Regression)는 하나 이상의 독립변수(X)를 이용해 연속형 목표 변수(Y)를 예측하는 가장 기본적인 지도학습 알고리즘

데이터를 가장 잘 대변하는 최적의 선을 찾는 과정
독립변수들(X)과 연속형 종속변수(Y) 사이의 선형 관계를 학습
장점
- 학습 및 예측 속도가 빠른 것이 특징
- 모델의 해석이 명확 (회귀계수 해석 가능)
단점
- X와 Y의 선형관계를 가정하기 때문에, 이러한 가정이 현실에서는 잘 적용되지 않을 가능성
- 이상치에 다소 민감

  
import pandas as pd
import statsmodels.api as sm

# 독립 변수(X), 상수항 추가
X = df[['X1', 'X2']]
X = sm.add_constant(X)  # 상수항 추가 (절편)
y = df['y'] # 종속 변수(y)

# OLS 모델 학습
model = sm.OLS(y, X).fit()
print(model.summary())

선형 회귀의 가정

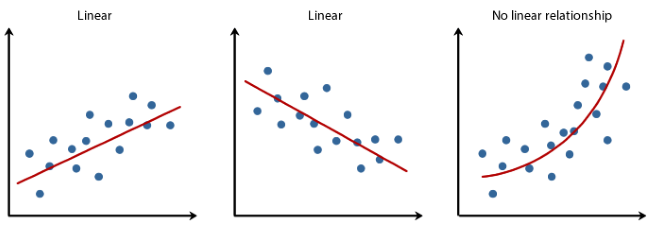
선형성: 독립변수(X) 와 종속변수(Y) 사이에는 선형 관계가 성립
주로 시각화를 통해 확인
해결방법: 로그변환, 제곱근 변환등으로 비선형성 완화

잔차 관련 가정

잔차(Residual) 관련 가정
- 정규성 : 잔차들은 평균이 0인 정규분포를 구성
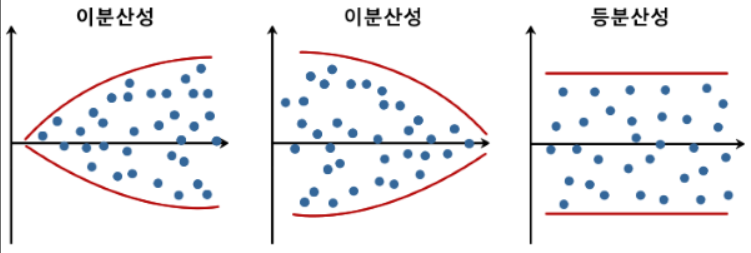
- 등분산성 : 잔차들의 분산은 일정 ➞ 회귀 분석의 신뢰성을 높이는 요소
만약 잔차 관련 가정이 위배된다면?
- 회귀계수의 신뢰 구간 및 가설 검정 결과의 부정확 동반
- 모델의 예측 능력 저하 증상
대표 확인 방법 : Q-Q(Quantile-Quantile) plot
- 잔차를 오름차순으로 나열 했을때의 분위수와 이론적인 잔차의 분위수 값을 비교해서 정규성을 확인

독립성

독립성 : 독립변수들(X) 간 상관관계(Correlation)가 존재하지 않아야 함
- 다중공선성 : 회귀 모형에 사용된 일부 독립변수가 다른 독립변수와 상관성이 높아, 모델 결과에 부정적 영향을 미치는 현상 → 독립성 가정이 위배되는 상황으로, 제거 필요

2. KNN

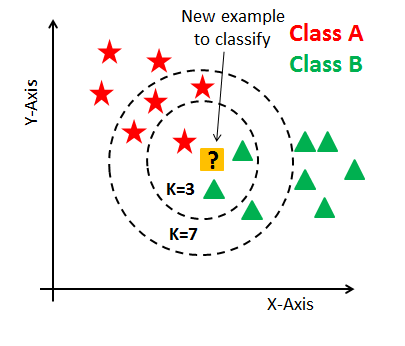
KNN(K-Nearest Neighbors)는 새로운 데이터 포인트가 주어졌을 때,
가장 가까운 K개의 이웃 데이터를 기준으로 예측값을 산출하는 비모수 기반 지도학습 알고리즘

가까운 이웃에 위치한 K개의 데이터를 보고, 데이터가 속할 그룹을 판단하는 과정
- 거리 기반 모델, 사례 기반 학습(Instance-Based Learning)
장점
- 단순하고, 특별한 훈련을 거치지 않아 빠르게 수행
- 데이터에 대한 특별한 가정이 존재 하지 않는 특징
단점
- 적절한 K 선택 필요
- 데이터가 많아지면 분류가 느려지는 현상
- 데이터 스케일에 민감하기에 스케일링이 필수적

  
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 독립 변수 / 종속 변수 분리
X = df[['X1', 'X2']]
y = df['y']

# Train/Test 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 스케일링
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# KNN 회귀 모델 정의 및 학습 (k=3)
model = KNeighborsRegressor(n_neighbors=3)
model.fit(X_train_scaled, y_train)

# 예측 및 평가
y_pred = model.predict(X_test_scaled)
rmse = mean_squared_error(y_test, y_pred, squared=False)
print(f"RMSE: {rmse:.4f}")

거리 측정 방법

KNN 알고리즘은 입력값과 가장 가까운 K개의 이웃을 찾기 때문에 “가깝다”는 개념을 정량화할 수 있는
거리 측정 방식(Metric)이 중요하다. 대표적인 거리 측정 방식으로는 다음과 같다.

유클리드 거리 (Euclidean Distance)

직선 거리(최단 경로)를 기준으로 측정
연속적인 공간에서 자주 사용됨
두 점 $A(x_1, y_1)$, $B(x_2, y_2)$ 사이의 유클리드 거리는 다음과 같다.

\[d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]

맨해튼 거리 (Manhattan Distance)

격자 형태(도시 블록, 픽셀 등)에서 주로 사용
차원 간 독립적 이동을 가정할 때 적합
두 점 $A(x_1, y_1)$, $B(x_2, y_2)$ 사이의 맨해튼 거리는 다음과 같다.

\[d(A, B) = |x_1 - x_2| + |y_1 - y_2|\]

K 값 결정

K값에 따라 고려하는 이웃 수가 달라지기 때문에 K값에 민감
주로 Cross Validation 을 통해 경험적으로 K 값을 선택

3. Decision Tree

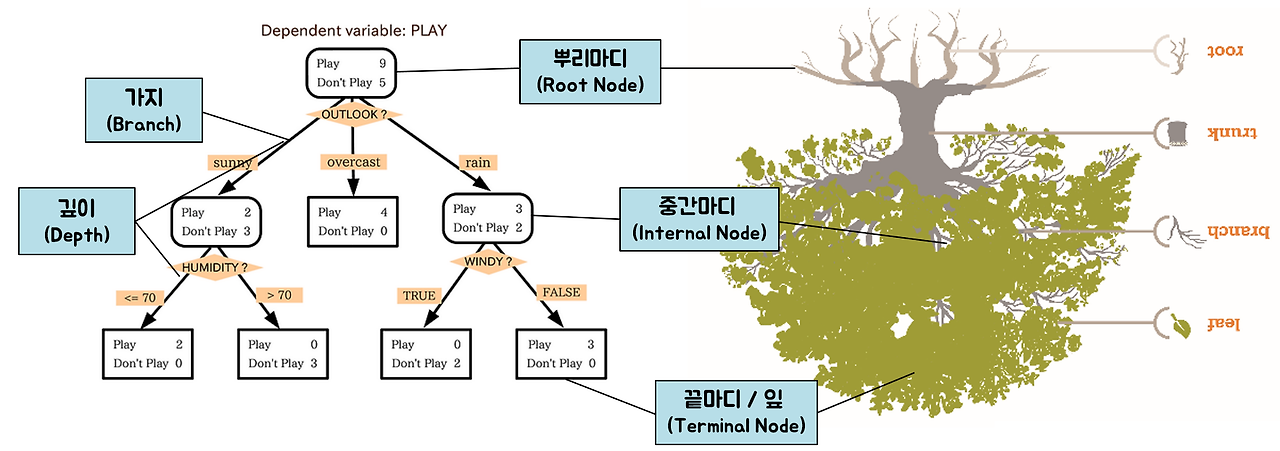
Decision Tree(의사결정나무)는 데이터를 여러 질문을 기준으로 분할해 나가며 트리 형태의 구조로 예측을 수행하는 지도학습 알고리즘이다.

데이터 내 규칙을 학습해, 조건에 따라 데이터를 분류하거나 회귀하는 방식
각 분기점(Node)에서는 특정 변수의 조건을 기준으로 데이터를 나눔
리프 노드(Leaf Node)에 도달하면 최종 예측값(클래스 or 수치)을 출력
모델 구조가 사람이 이해하기 쉬워 해석 가능성(Explainability)이 높음

장점
- 직관적으로 이해가 쉽고, 데이터 스케일에 민감하지 않음
- 범주형과 연속형 데이터를 모두 처리 가능
단점
- 트리 깊이가 깊어지면 과적합의 위험 존재 → 적절한 Pruning이 필요
- 새로운 Sample에 취약할 수 있음

  
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 학습
model = DecisionTreeClassifier(max_depth=5, random_state=42)
model.fit(X_train, y_train)

# 예측 및 평가
y_pred = model.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Accuracy: {acc:.2f}")

가지치기(Pruning)

트리의 깊이(Depth)가 깊어지거나 Leaf가 많아지면 과적합의 위험이 커진다는 단점을 보완하기 위함
형성된 결정트리의 특정 노드 아래 트리나 Leaf를 제거해 일반화 성능을 높이기 위한 전략

Tree Depth 조절

과적합 방지에 중요한 것은 트리의 Depth(깊이)와 Leaf(노드)를 적절히 조정하는 것
가지치기 이외에도 아래처럼 sklearn에는 트리 깊이와 노드를 조정할 수 있는 Hyperparameter가 존재

Max depth : 트리의 최대 깊이
Max Leaf Nodes : 최대 몇개 Leaf 노드가 만들어 질 때까지 split 할건지?
Min sample split : 최소 샘플이 몇개 이상이어야 하위 노드로 split 할건지?

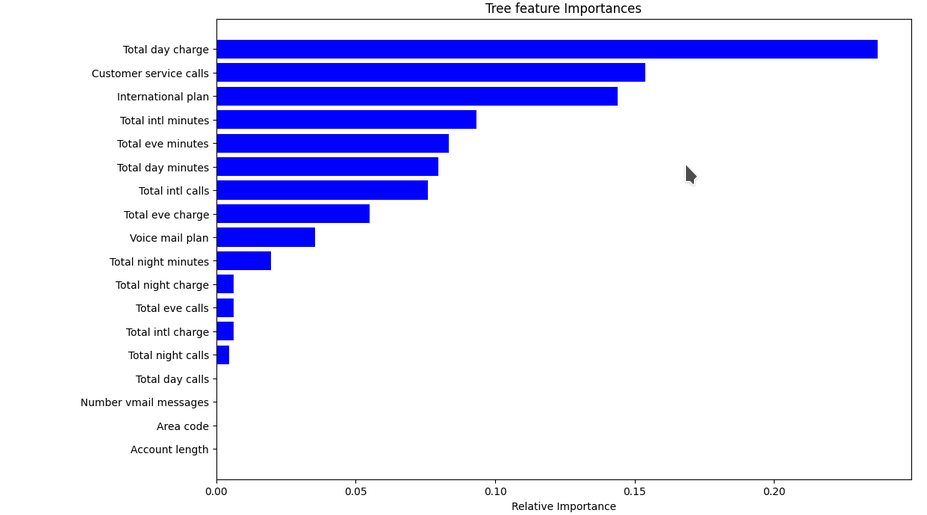
Feature Importance

트리 분기 과정에서 불순도를 많이 낮출 수 있는 feature = 중요한 feature
Feature selection의 기준으로 활용되기도 함
해당 지표는 절대적이지 않음에 유의
분할 기준, 모델 학습 과정 등에 따라 달라질 수 있음

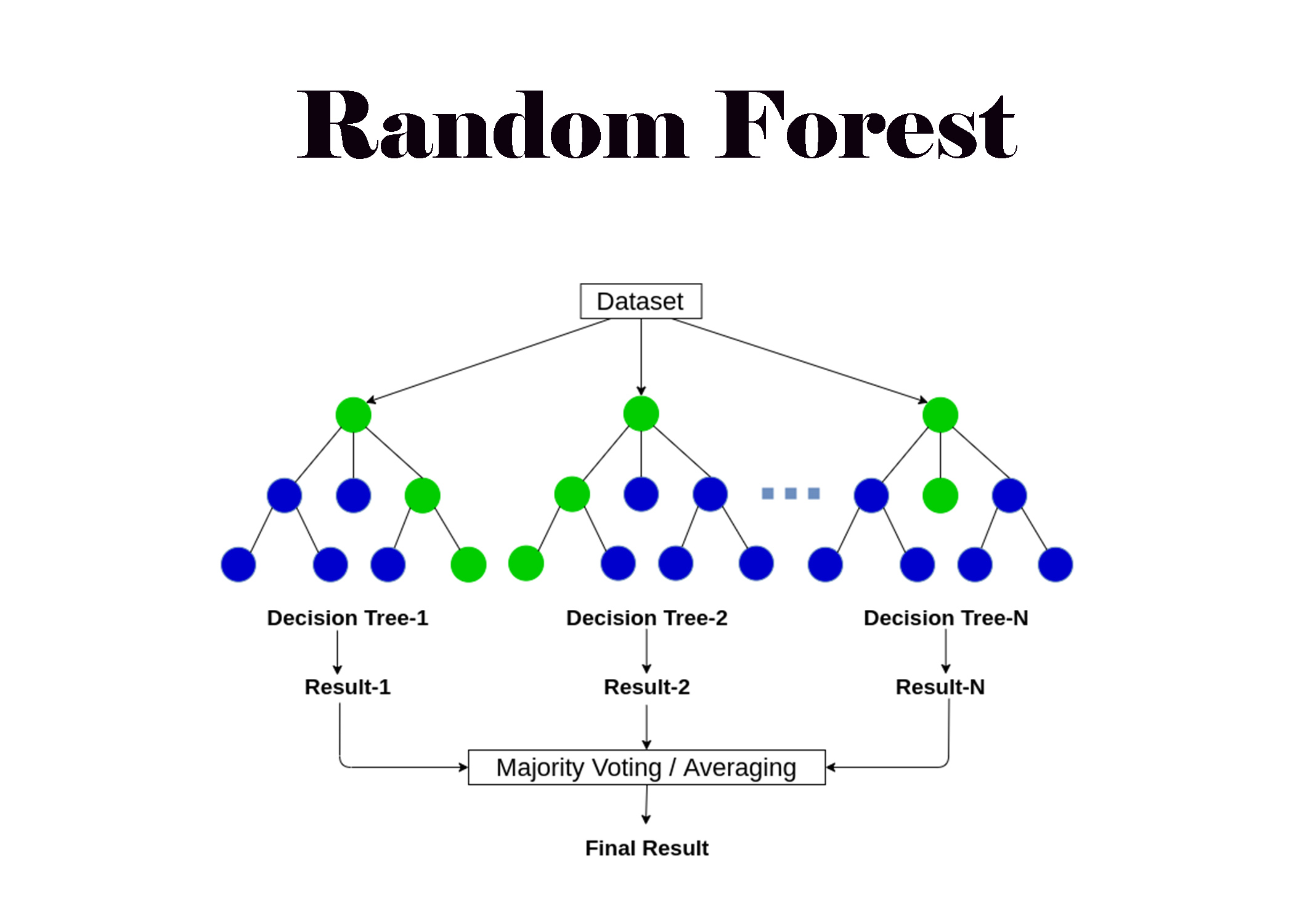
4. Random Forest

Random Forest는 여러 개의 결정 트리를 학습시키고, 이들의 예측을 앙상블(다수결 or 평균)하여 최종 결과를 도출하는 앙상블 기반 지도학습 알고리즘이다.

트리 앙상블(Tree Ensemble): 대표적으로 배깅(Bagging), 부스팅(Boosting) 방법이 존재
각 트리는 학습 시 데이터 샘플과 변수 일부를 무작위로 선택하여 생성
이를 통해 과적합을 줄이고 일반화 성능을 향상시킨다.

장점
- 부트스트랩으로 인해, 단일 의사결정나무의 단점인 높은 분산이 줄어 예측 성능 향상 기대
- 여러 트리의 융합으로 과적합 완화 기대
- 그 외 의사결정나무의 장점을 모두 흡수
단점
- 데이터 크기에 비례해 N개의 트리를 생성하기에, 대용량 데이터 학습의 경우 오랜 시간 소요
- 생성하는 모든 트리를 모두 확인하기 어려워, 해석 가능성이 단일 트리모델보다 떨어지는 문제

  
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 학습
model = RandomForestClassifier(n_estimators=100, max_depth=None, random_state=42)
model.fit(X_train, y_train)

# 예측 및 평가
y_pred = model.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Accuracy: {acc:.2f}")

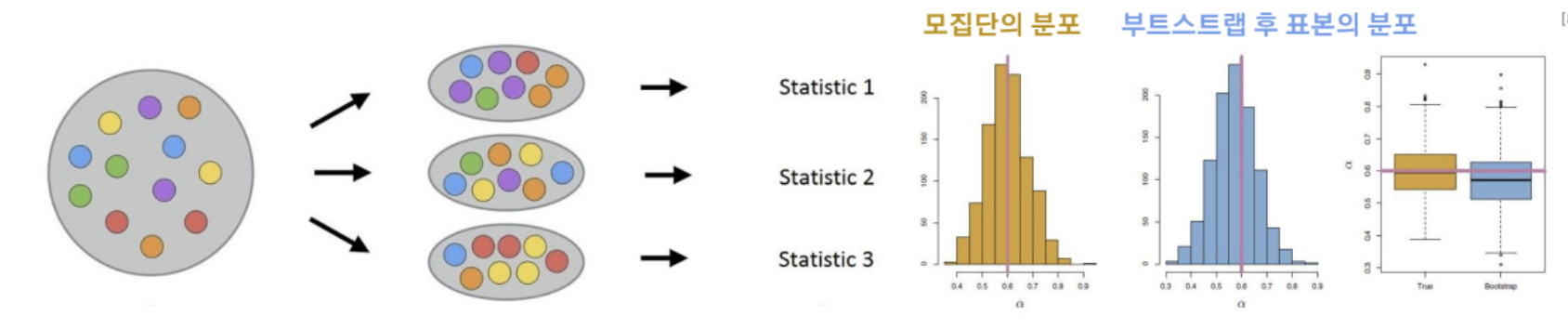
Bootstrap

부트스트랩(Bootstrap) : 복원추출을 사용해 표본을 추출해 모집단의 통계량을 추론하는 통계적 방법
여기서 각 표본들은 복원추출로 생성되었으므로 독립적

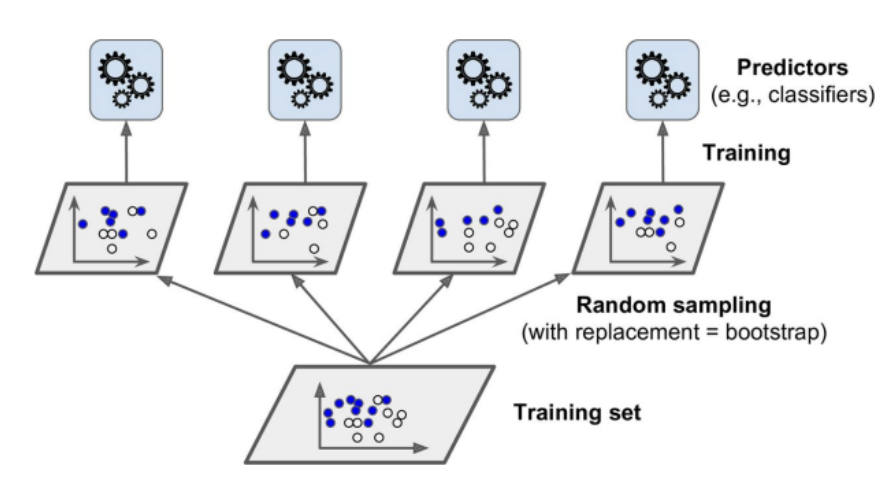
Bagging

앞선 부트스트랩의 복원추출 과정을 머신러닝 앙상블에 사용
부트스트랩을 통해 표본을 여러번 뽑아 모델을 학습시키고, 그 결과를 집계(Aggregation) 하는 앙상블 방법

AI | 인공지능, Upstage AI Lab

Machine Learning

This post is licensed under CC BY 4.0 by the author.