[Upstage AI Lab] 3주차 - Statistics

들어가며

이번 주는 통계 수업이 마무리되며, 3주차 학습이 마무리되었다.
이번 포스팅에서는 이러한 학습 내용을 바탕으로 3주차 학습 내용을 요약 및 정리했다.

1. 유사도 & 거리 척도

---

1-1. 유클리드 거리

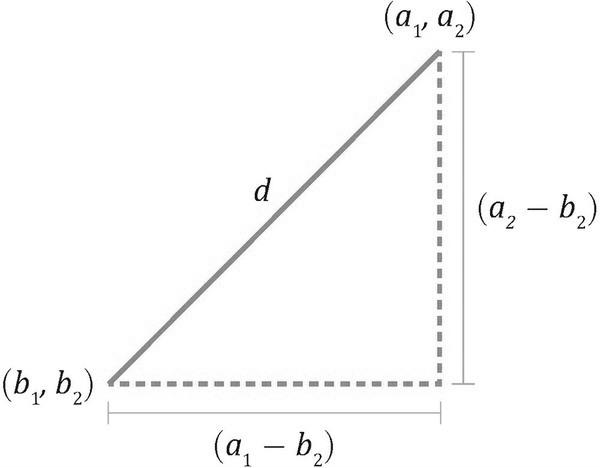
유클리드 거리 예시

\[d(x, y) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots + (x_n - y_n)^2}\]

• 군집 분석의 척도 중 가장 일반적이고 직관적인 거리 측정 방법
• 두 점 사이의 가장 짧은 직선 거리 (직각삼각형의 빗변)
• 피타고라스 정리 기반
• L2 거리(L2 Norm)라고도 불림
• K-최근접 이웃(KNN), K-Means 군집분석, PCA 거리 기반 차원 축소 등 사용

PyTorch로 구현

# 유클리드 유사도의 코드 표현 
euclidean_distance = torch.norm(b - c, p = 2) # 유클리드 거리 계산
euclidean_similarity = 1 / (1 + euclidean_distance) # 유사도 계산 (예시: 거리의 역수)

print(f'Euclidean Distance: {euclidean_distance.item()}')
print(f'Euclidean Similarity: {euclidean_similarity.item()}')

Euclidean Distance: 1.4142135381698608
Euclidean Similarity: 0.41421353816986084

1-2. 맨해튼 거리

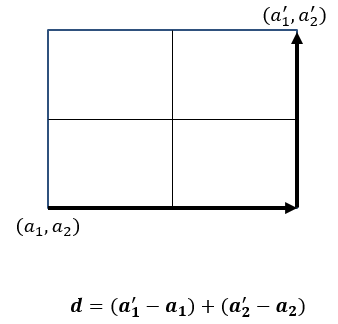
맨해튼 거리 예시

\[d(x, y) = |x_1 - y_1| + |x_2 - y_2| + \cdots + |x_n - y_n|\]

• 격자형 도로 위에서 두 지점을 이동할 때 총 거리
• 직선이 아닌, 축을 따라 이동하는 거리의 총합
• L1 거리(L1 Norm)이라고도 불림
• 이상치에 덜 민감하여 강건한 모델에 유리
• 텍스트 데이터 분석, 추천 시스템, 군집 분석 등에서 활용

PyTorch로 구현

# 맨해튼 유사도의 코드 표현 실습
b = torch.tensor([1, 0, 2], dtype=torch.float32)
c = torch.tensor([0, 1, 2], dtype=torch.float32)

manhattan_distance = torch.norm(b - c, p = 1) # 맨해튼 거리 계산
manhattan_similarity = 1 / (1 + manhattan_distance) # 유사도 계산 (예시: 거리의 역수)

print(f'Manhattan Distance: {manhattan_distance}')
print(f'Manhattan Similarity: {manhattan_similarity}')

Manhattan Distance: 2.0
Manhattan Similarity: 0.3333333432674408

1-3. 코사인 거리

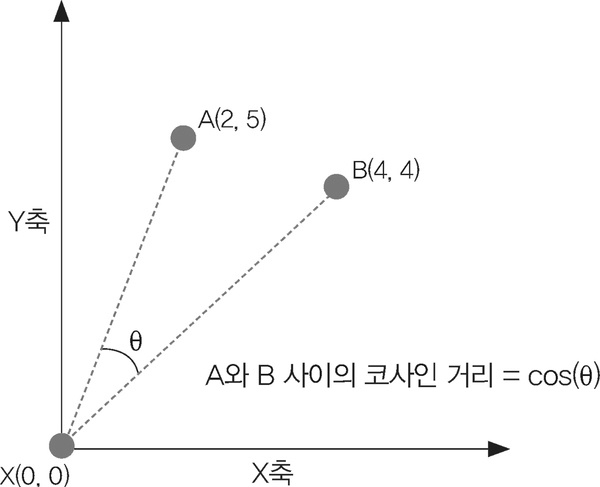
코사인 거리 예시

\[d(x, y) = 1 - \frac{\vec{x} \cdot \vec{y}}{\|\vec{x}\| \cdot \|\vec{y}\|}\]

• 두 벡터 사이의 각도를 기준으로 유사도를 측정
• 거리 자체보다는, 벡터가 얼마나 비슷한 방향을 갖는지가 중요
• 문서 간 유사도, 텍스트 마이닝 등에서 매우 자주 사용됨
• 단위 크기와 무관, 크기보다 방향성이 중요한 문제에 적합

PyTorch로 구현

# 코사인 유사도의 코드 표현
dot_product = torch.dot(b, c)
norm_b = torch.norm(b, p = 2)
norm_c = torch.norm(c, p = 2)
cosine_similarity = dot_product / (norm_b * norm_c) 

print(f'Cosine Similarity: {cosine_similarity.item()}')

Cosine Similarity: 0.800000011920929

2. 통계적 가설 검정

---

• 정규성 검정, T 검정, ANOVA 검정, 상관분석에 대한 내용을 정리했다.
• 아래는 Python으로 구현한 예제 코드이다.

2-1. Library

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import platform
import warnings
import pingouin as pg
from matplotlib import font_manager, rc
from scipy import stats
from scipy.stats import shapiro, f_oneway

warnings.filterwarnings('ignore')

path = '/library/Fonts/Arial Unicode.ttf'
if platform.system() == 'Darwin':
    print('Hangul OK in your MAC!')
    rc('font', family='Arial Unicode MS')
elif platform.system() == 'Windows':
    font_name = font_manager.FontProperties(fname=path).get_name()
    rc('font', family=font_name)
else:
    print('Unknown system.. sorry')
plt.rcParams['axes.unicode_minus'] = False

Hangul OK in your MAC!

# Data load
df = sns.load_dataset('tips') # tip 관련 데이터 
df

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4
...	...	...	...	...	...	...	...
239	29.03	5.92	Male	No	Sat	Dinner	3
240	27.18	2.00	Female	Yes	Sat	Dinner	2
241	22.67	2.00	Male	Yes	Sat	Dinner	2
242	17.82	1.75	Male	No	Sat	Dinner	2
243	18.78	3.00	Female	No	Thur	Dinner	2

244 rows × 7 columns

2-2. Normality 검정

num_df = df.select_dtypes(include=['number'])

for col in num_df.columns:
    shap, p_value = stats.shapiro(num_df[col])

    if p_value > 0.05:
        print(f"정규성 만족: {col}은 정규분포를 따른다.")
    else:
        print(f"정규성 불만족: {col}은 비정규분포를 따른다.")

정규성 불만족: total_bill은 비정규분포를 따른다.
정규성 불만족: tip은 비정규분포를 따른다.
정규성 불만족: size은 비정규분포를 따른다.

# 시각화 확인
plt.figure(figsize=(8, 6))
sns.histplot(df['total_bill'], kde=True)
plt.show()

2-3. T-검정

• 단일표본 t 검정
• 독립표본 t 검정

# 손님들이 주는 팁의 평균이 3달러 인가?
t_stat, p_value = stats.ttest_1samp(df['tip'], 3) # 단일표본 검정
print(f"T-stat: {t_stat:.4f}, P-value: {p_value:.4f}")

if p_value > 0.05:
    print(f"귀무가설 채택 → 평균 팁은 3달러와 유의한 차이가 없음 (P-value={p_value:.4f})")
else:
    print(f"귀무가설 기각 → 평균 팁은 3달러와 유의하게 다름 (P-value={p_value:.4f})")

T-stat: -0.0194, P-value: 0.9845
귀무가설 채택 → 평균 팁은 3달러와 유의한 차이가 없음 (P-value=0.9845)

# 흡연자와 비흡연자의 평균 팁 금액 차이가 있는가?
smokers = df[df['smoker'] == 'Yes']['tip'] # 흡연자
non_smokers = df[df['smoker'] == 'No']['tip'] # 비흡연자

t_stat, p_value = stats.ttest_ind(smokers, non_smokers) # 독립표본 t검정
print(f"T-stat: {t_stat:.4f}, P-value: {p_value:.4f}")

if p_value > 0.05:
    print(f"귀무가설 채택 → 흡연자와 비흡연자의 평균 팁에 유의한 차이 없음(P-value={p_value:.4f})")
else:
    print(f"귀무가설 기각 → 흡연자와 비흡연자의 평균 팁에 유의한 차이 있음(P-value={p_value:.4f})")

T-stat: 0.0922, P-value: 0.9266
귀무가설 채택 → 흡연자와 비흡연자의 평균 팁에 유의한 차이 없음(P-value=0.9266)

2-4. ANOVA 검정

• One-way ANOVA(일원 분산분석)
• Two-way ANOVA(이원 분산분석)

# 점시과 저녁의 팁 차이가 있는가?
lunch = df[df['time'] == 'Lunch']['tip'] # 점심
dinner = df[df['time'] == 'Dinner']['tip'] # 저녁
stat, p_value = stats.f_oneway(lunch, dinner) # 일원 분산분석
print(f"Stat: {stat:.4f}, P-value: {p_value:.4f}")

if p_value > 0.05:
    print(f"귀무가설 채택 → 점심과 저녁의 팁에 유의한 차이 없음 (P-value={p_value:.4f})")
else:
    print(f"귀무가설 기각 → 점심과 저녁의 팁에 유의한 차이 있음 (P-value={p_value:.4f})")

Stat: 3.6338, P-value: 0.0578
귀무가설 채택 → 점심과 저녁의 팁에 유의한 차이 없음 (P-value=0.0578)

해석

항목	의미
SS	제곱합 (Sum of Squares) → 각 요인이 설명하는 변동량
DF	자유도 (Degree of Freedom)
MS	평균제곱 (Mean Square) = SS / DF
F	F-통계량 (요인의 영향력 크기 비교)
p-unc	p-value (유의확률)
np2	eta-squared (효과크기, 설명력 비율)

# 성별과 요일에 따른 팁 차이가 있는가?
anova_result = pg.anova(dv='tip', between=['sex', 'day'], data=df) # 이원 분산분석
print(f"{anova_result}\n")

# 유의확률(p-value) 기준으로 해석
for i, row in anova_result.iterrows():
    factor = row['Source']
    
    if factor == 'Residual':  # Residual 스킵
        continue

    pval = row['p-unc']
    if pval > 0.05:
        print(f"귀무가설 채택 → '{factor}'에 따른 팁의 평균 차이는 유의하지 않음 (P-value={pval:.4f})")
    else:
        print(f"귀무가설 기각 → '{factor}'에 따른 팁의 평균 차이에 유의한 차이가 있음 (P-value={pval:.4f})")

      Source          SS     DF        MS         F     p-unc       np2
0        sex    1.594561    1.0  1.594561  0.833839  0.362097  0.003521
1        day    7.446900    3.0  2.482300  1.298061  0.275785  0.016233
2  sex * day    2.785891    3.0  0.928630  0.485606  0.692600  0.006135
3   Residual  451.306151  236.0  1.912314       NaN       NaN       NaN

귀무가설 채택 → 'sex'에 따른 팁의 평균 차이는 유의하지 않음 (P-value=0.3621)
귀무가설 채택 → 'day'에 따른 팁의 평균 차이는 유의하지 않음 (P-value=0.2758)
귀무가설 채택 → 'sex * day'에 따른 팁의 평균 차이는 유의하지 않음 (P-value=0.6926)

2-5. 상관분석

• pearsonr
• spearmanr

# Pearson 상관분석 (선형 관계)
pearson_corr, pearson_p = stats.pearsonr(df['total_bill'], df['tip'])
print(f"상관계수: {pearson_corr:.4f}, P-value: {pearson_p:.4f}")

# 유의성 해석
if pearson_p > 0.05:
    print(f"귀무가설 채택 → 'total_bill'과 'tip' 사이에 선형 상관관계 없음 (P-value={pearson_p:.4f})")
else:
    print(f"귀무가설 기각 → 'total_bill'과 'tip' 사이에 선형 상관관계 있음 (P-value={pearson_p:.4f})")

상관계수: 0.6757, P-value: 0.0000
귀무가설 기각 → 'total_bill'과 'tip' 사이에 선형 상관관계 있음 (P-value=0.0000)

# 시각화
plt.figure(figsize=(8, 6))
sns.regplot(x='total_bill', y='tip', data=df, line_kws={'color': 'red'}, scatter_kws={'alpha': 0.6})
plt.title("Total Bill vs Tip (with Regression Line)")
plt.xlabel("Total Bill")
plt.ylabel("Tip")
plt.grid(True)
plt.tight_layout()
plt.show()

• Spearman 상관 분석은 데이터의 순위를 기반으로 관계를 분석하는 비모수 통계 기법
• 시각화 시 회귀선을 그리지 않는 이유는, 직선 회귀는 수치 간 선형 관계를 전제로 하기 때문
• 스피어만은 단조한 순위 관계를 보기 때문에 선형 회귀선이 의미 없다.

# Spearman 상관분석
spearman_corr, spearman_p = stats.spearmanr(df['total_bill'], df['tip'])
print(f"상관계수: {spearman_corr:.4f}, P-value: {spearman_p:.4f}")

# 유의성 판별
if spearman_p > 0.05:
    print(f"귀무가설 채택 → total_bill과 tip 간의 순위 상관은 유의하지 않음 (P-value={spearman_p:.4f})")
else:
    print(f"귀무가설 기각 → total_bill과 tip 간의 순위 상관에 유의한 관계가 있음 (P-value={spearman_p:.4f})")

상관계수: 0.6790, P-value: 0.0000
귀무가설 기각 → total_bill과 tip 간의 순위 상관에 유의한 관계가 있음 (P-value=0.0000)

# 순위로 변환
df['rank_total_bill'] = df['total_bill'].rank()
df['rank_tip'] = df['tip'].rank()

# 시각화
plt.figure(figsize=(8, 6))
plt.scatter(df['rank_total_bill'], df['rank_tip'])
plt.title('Spearman Rank Correlation (순위 기준)')
plt.xlabel('Rank of total_bill')
plt.ylabel('Rank of tip')
plt.grid(True)
plt.show()