[Upstage AI Lab] 2주차 - Data Analysis

들어가며

이번 주는 김인섭 강사님의 실시간 강의로 Python, 데이터분석 까지 다졌고 금요일부터는 오영석 강사님의 통계 수업이 시작되며 2주차 학습이 마무리되었다. 이번 포스팅에서는 이러한 학습 내용을 바탕으로 2주차 학습 내용을 요약 및 정리했다.

1. Pandas

---

Pandas는 데이터 처리를 지원하는 Python의 라이브러리이다. 인덱싱, 연산용 함수, 전처리 함수 등을 제공하며 데이터 분석, 통계 분석 등을 위해 사용한다.

1-1. Series

• 하나의 정보에 대한 데이터들의 집합
• 1개의 컬럼값으로 구성된 1차원 데이터 셋

import pandas as pd

data = ["A", "B", "C", "D", "E"] # 컬럼
se = pd.Series(data)
se

0    A
1    B
2    C
3    D
4    E
dtype: object

se[0] # indexing -> A
se[:3] # slicing

0    A
1    B
2    C
dtype: object

se.name = "alphabet" # series 이름
se.index.name = "No." # index 이름

se

No.
0    A
1    B
2    C
3    D
4    E
Name: alphabet, dtype: object

1-2. DataFrame

• 데이터 분석에서 가장 중요한 데이터 구조
• 관계형 데이터베이스의 테이블 또는 엑셀 시트와 같은 형태(2차원 구조)
• ✅스테로이드를 맞은 엑셀 이라고도 불림

데이터 생성

data = {
    'country' : ["kor", "usa", "china", "japan"],
    'rank' : [1,2,3,4],
    'grade' : ["A", "B", "C", "D"],}

df = pd.DataFrame(data)
df

	country	rank	grade
0	kor	1	A
1	usa	2	B
2	china	3	C
3	japan	4	D

데이터 추가 및 삭제

president = pd.Series(["yoon", "biden", "jinping", "kishida"])
president

df['president'] = president # 추가
df

	country	rank	grade	president
0	kor	1	A	yoon
1	usa	2	B	biden
2	china	3	C	jinping
3	japan	4	D	kishida

df.drop(columns=['grade'], inplace=True) # inplace=True는 원본 df에서 컬럼을 제거하여 바로 반영
df = df.drop(columns=['grade']) # 이 방법으로도 가능

	country	rank	president
0	kor	1	yoon
1	usa	2	biden
2	china	3	jinping
3	japan	4	kishida

# DataFrame 재생성
data = {'country': ["kor", "usa", "china", "japan"],
        'rank': [1, 2, 3, 4],
        'grade': ["A", "B", "C", "D"],
        'score': [100, 80, 60, 40]
        }

df = pd.DataFrame(data)
df

	country	rank	grade	score
0	kor	1	A	100
1	usa	2	B	80
2	china	3	C	60
3	japan	4	D	40

결측치 처리

• NaN : Not a Number (=> 비어있는 데이터, None, Null)
• isnull(): True
• isna(): isnull() 과 동일
• fillna(): null인 데이터들을 내가 입력하는 어떤 값으로 채움
• dropna(): null 데이터를 제거

# 결측치 생성
df['check'] = np.nan
df

	country	rank	grade	score	check
0	kor	1	A	100	NaN
1	usa	2	B	80	NaN
2	china	3	C	60	NaN
3	japan	4	D	40	NaN

결측치 확인

df.isna()

	country	rank	grade	score	check
0	False	False	False	False	True
1	False	False	False	False	True
2	False	False	False	False	True
3	False	False	False	False	True

df.isna().sum()

country    0
rank       0
grade      0
score      0
check      4
dtype: int64

결측치 제거

df = df.dropna()
# df = df.fillna(대체할 값) < 결측치 대체
df.isna().sum()

country    0
rank       0
grade      0
score      0
check      0
dtype: int64

1-3. Merge

• merge()는 두 개 이상의 데이터프레임을 특정 열(또는 열들)을 기준으로 합칠 때 사용
• DB 테이블 조인과 유사하게 병합할 수 있다.
• 매개변수: on, how, left, right 등

data = {
    "고객번호" : [1001, 1002, 1003, 1004],
    '이름': ['LG', "Samsung", "Hyundai", "Kia"]}

df1 = pd.DataFrame(data)
df1

	고객번호	이름
0	1001	LG
1	1002	Samsung
2	1003	Hyundai
3	1004	Kia

data = {
    "고객번호" : [1001, 1001, 1005, 1006],
    '시총': ['10조', "5조", "3조", "1조"]}

df2 = pd.DataFrame(data)
df2

	고객번호	시총
0	1001	10조
1	1001	5조
2	1005	3조
3	1006	1조

df = pd.merge(df1, df2, how='outer')
df

	고객번호	이름	시총
0	1001	LG	10조
1	1001	LG	5조
2	1002	Samsung	NaN
3	1003	Hyundai	NaN
4	1004	Kia	NaN
5	1005	NaN	3조
6	1006	NaN	1조

1-3. Concat

• concat() 함수는 여러 개의 데이터프레임을 행 또는 열 방향으로 간단히 연결하고자 할 때 사용
• 데이터프레임을 위아래로 쌓아 올리거나 좌우로 이어붙일 수 있다.

df1 = pd.DataFrame({"A": [1,2], "B": [3,4]})
df2 = pd.DataFrame({"A": [3,4], "B": [5,6]})

# 세로로 합치기
df_concat = pd.concat([df1, df2], ignore_index=True)
df_concat

	A	B
0	1	3
1	2	4
2	3	5
3	4	6

df1 = pd.DataFrame({'A': [1, 2], 'B': [3, 4]})
df2 = pd.DataFrame({'C': [5, 6], 'D': [7, 8]})

# 가로로 합치기
result = pd.concat([df1, df2], axis=1)
result

	A	B	C	D
0	1	3	5	7
1	2	4	6	8

2. Statistics

---

이번 강의에서는 Statistics의 기초 개념과 원리, 방법을 학습한다고 한다.
또한 Python 과 PyTorch 프레임워크를 활용하여 데이터를 표현하고 처리하는 실습을 진행한다.

2-1. 순열(Permutation)

순열의 언어적 표현

• 순열(Permutation)이란? 주어진 집합의 원소들을 특정한 순서로 배열하는 방법을 의미함
  • 예) 집합{𝐴,𝐵}가 있을 때 가능한 순열은 𝐴𝐵 와 𝐵𝐴
• 순열에서는 원소의 순서가 매우 중요하며, 순서가 바뀌면 서로 다른 순열로 간주함
  • 예1) 주어진 집합{𝐴,𝐵}에서의 𝐴𝐵와 𝐵𝐴는 서로 다른 순열

순열의 수에 대한 수식 표현

• 전체 수열: 서로 다른 n개의 원소로 만들 수 있는 모든 순열의 수는 n!로 계산된다.
• n 팩토리얼: 1부터 n까지 자연수를 차례로 곱한 것을 n팩토리얼, 기호로는 n!과 같이 표기

\[P(n, r) = \frac{n!}{(n - r)!}\]

코드 표현

• itertools: Python의 표준 라이브러리 모듈 중 하나로, 효율적인 반복을 위한 다양한 함수와 도구들을 제공
• 반복자(iterators)를 생성하고 조합하여 복잡한 반복작업을 단순하고 효율적으로 수행할 수 있게 도와줌

import itertools

# 1, 2, 3, 4 숫자가 적힌 카드가 있다고 가정
lists = [1, 2, 3, 4]

# 카드 중 두 장 꺼내는 경우
a = list(itertools.permutations(lists, 2))

print(a)
len(a) # 12

2-2. 조합(Combination)

조합의 언어적 표현

• 조합(Combination)이란 주어진 집합에서 순서에 상관없이 일부 원소들을 선택하는 방법을 의미함
  • 예) 집합 {𝐴,𝐵}가 있을 때 가능한 조합은
    • 원소하나를선택하는경우 𝐴,𝐵
    • 원소 두개를 선택하는 경우 𝐴𝐵(즉, 조합에서는 𝐴𝐵, 𝐵𝐴를 동일한 것으로 취급)

조합의 수에 대한 수식 표현

• 서로 다른 n개 중 r개를 순서 없이 고르는 경우의 수

\[C(n, r) = \frac{n!}{r!(n - r)!}\]

import itertools

# 리스트를
cards = [1, 2, 3, 4]

# 2개씩 뽑는 조합 생성 (순서 고려하지 않음)
b = list(itertools.combinations(cards, 2))

print(b)  # [(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)]
print(len(b)) # 6

2-3. 확률의 용어

• 시행: 동일한 조건에서 반복할 수 있으며, 그 결과가 우연에 의해 결정되는 관찰이나 실험
  • ex) 주사위 던지기, 동전 던지기
• 표본공간: 시행에서 나타날 수 있는 모든 가능한 결과들의 전체 집합
  • ex) 주사위를 1회 던졌을 때 표본공간은{1,2,3,4,5,6}
• 근원사건: 표본공간을 구성하는 각각의 개별적인 결과, 즉 실험이나 시행에서 일어날 수 있는 단일한 사건
  • ex) 주사위를 1회 던졌을 때, 근원사건 : 1, 2, 3, 4, 5, 6
• 사건: 표본공간 내의 근원사건들의 집합으로, 특정 실험이나 시행에서 발생할 수 있는 결과들의 부분집합
  • ex) 주사위를 1회 던졌을 때, 홀수가 나올사건 : {1,3,5}

합사건

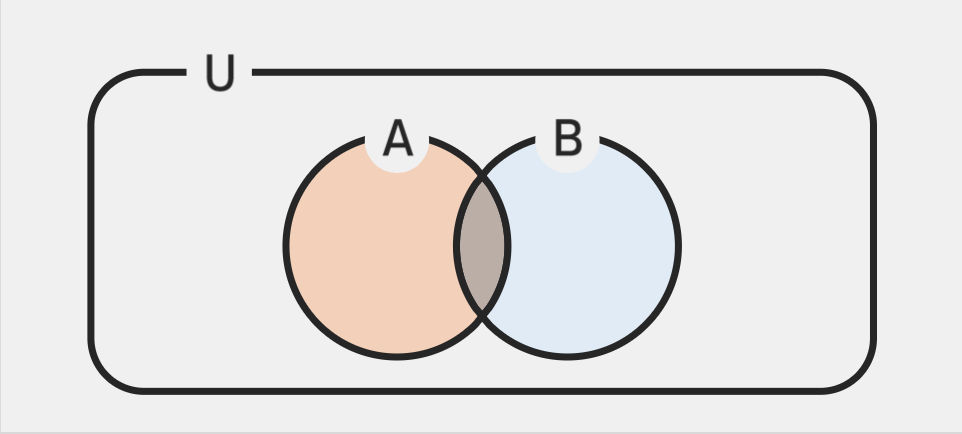
• 사건 𝐴와 𝐵에 대해 𝐴또는 𝐵가 발생하는 사건, 즉 둘 중 하나라도 발생하는 경우를 포함하는사건
  • ex) 비가 오거나 눈이 오는 날 → 둘 중 하나라도 일어나는 날 == or

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

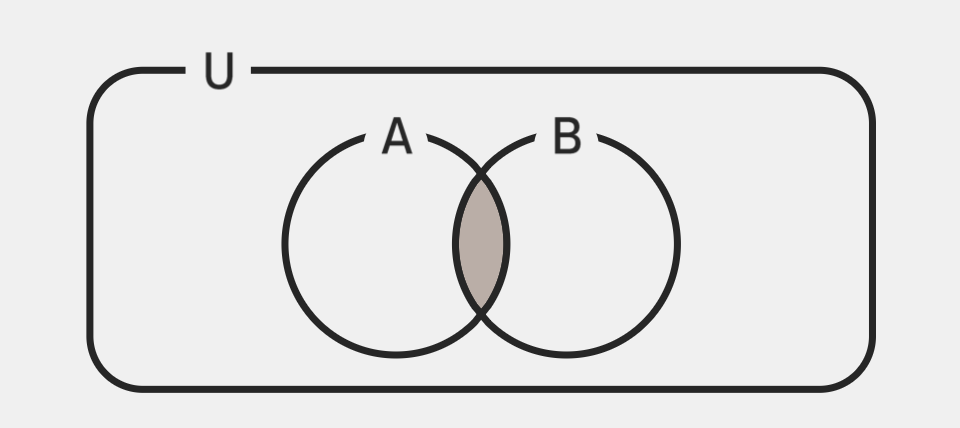
곱사건

• 사건 A와 B에 대해 A와 B가 모두 동시에 발생하는 사건
  • ex) 곱사건 == 교집합 and

\[P(A \cap B) = P(A) \cdot P(B|A)\]

(독립 사건일 경우)
\(P(A \cap B) = P(A) \cdot P(B)\)

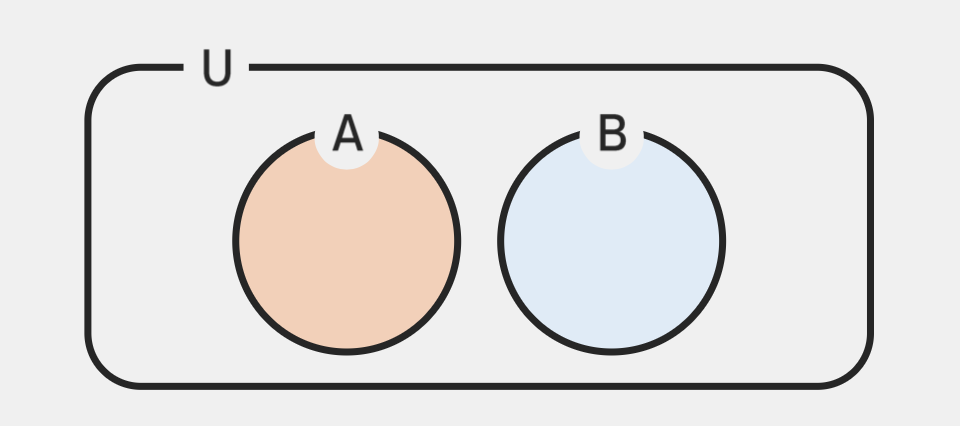
배반사건

• 사건 𝐴와 𝐵에 대해 𝐴와 𝐵가 동시에 발생할 수 없고, 하나가 발생하면, 다른 하나는 반드시 발생하지 않는사건

\[P(A \cap B) = 0\]

⇒ 따라서
\(P(A \cup B) = P(A) + P(B)\)

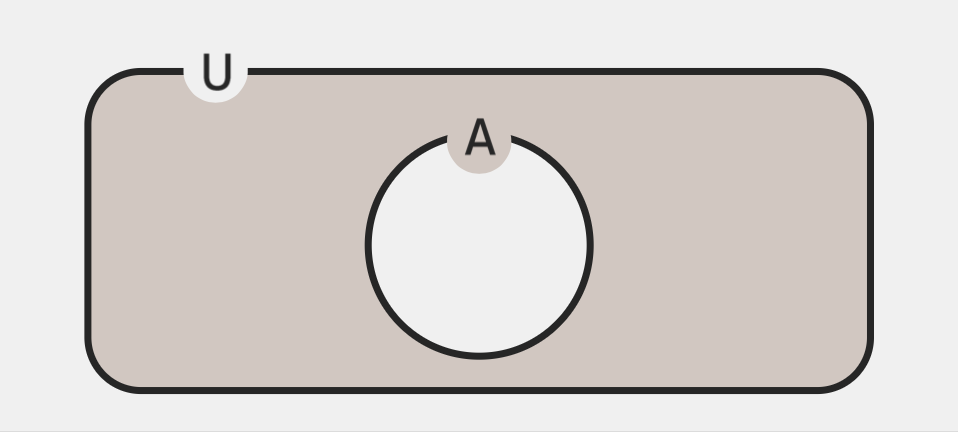
여사건

• 사건 𝐴에 대해 𝐴가 일어나지 않는 경우에 해당하는 사건
  • ex) 주사위 예시
    • 전체 사건: 주사위 눈 1, 2, 3, 4, 5, 6
    • 사건 A: “3 이하가 나올 확률” → {1, 2, 3}
    • 여사건 A’: “3 이하가 아닌 눈이 나올 확률” → {4, 5, 6}
    • 즉 P(A) = 3/6 = 0.5 => P(A) = 1 - 0.5 = 0.5

\[P(A') = 1 - P(A)\]

2-5. 조건부 확률

• 사건 𝐴와 사건𝐵가 발생하는 과정에 순서 개념이 없다.
• 하지만 사건 𝐴가 발생한 상황 하에 사건𝐵가 발생할 확률을 구하고자 할때 조건부 확률을 구하게 된다.
• 𝑃(𝐵ㅣ𝐴)로 표기

\[P(B \mid A) = \frac{P(B \cap A)}{P(A)}\]

예시(ex)

어느 회사의 주가가 월요일 장에 상승할 확률이 0.7이라고 하며, 월요일에 상승하고 그 다음 날에도 상승할 확률이 0.3이라고 한다. 어느 특정 월요일에 주가가 올랐다면 그 다음 날에도 다시 주가가 오를 확률은?

𝐴 =월요일에주가가오를사건, 𝐵 =화요일에주가가오를사건

\[P(B \mid A) = \frac{P(A \cap B)}{P(A)} = \frac{0.3}{0.7} = \frac{3}{7}\]

2-6. 독립사건

• 두 사건𝐴와 𝐵에서 한 사건의 결과가 다른 사건에 영향을 주지 않을 때
• 𝐴와 𝐵를 독립사건이라고 하며 다음과 같이 표현

\[P(B \mid A) = P(B \mid A^c) = P(B)\] \[P(B \cap A) = P(A) \cdot P(B \mid A) = P(A) \cdot P(B)\]

2-7. 종속 사건

• 두 사건𝐴와 𝐵에서 한 사건의 결과가 다른 사건에 영향을 줄 때
• 𝐴와 𝐵를 종속사건이라고 하며 다음과 같이 표현

\[P(B \mid A) \ne P(B \mid A^c) \ne P(B)\]

2-8. 척도

• 범주형 척도와 연속형 척도로 분리
• 범주형 척도: 데이터들을 구분 지어 나눌 수 있는 척도로서, 명목척도와 서열척도로 구분
• 연속형 척도: 연속하는 속성의 데이터를 연구나 조사의 목적에 맞게 구분한 척도로서, 등간척도와 비율척도로 구분

• 명목척도: 명목척도는 수나 순서와 관계없이 이름만 붙여지는 척도
• 서열척도: 명목척도와 유사하게 숫자나 연산과는 관련 없으나, 순서(서열)를 구분할 수 있는 척도
• 등간척도: 명목척도 또는 서열척도와는 달리, 측정한 자료들을 대상으로 합과 차가 가능한 척도
• 비율척도: 등간척도의 성질과 함께 없다의 개념인 0값도 가지는 척도

2-9. 모집단

• 모집단: 통계적 연구대상이 되는 전체 집합
  • ex) 모든 대한민국 국민
  • ex) 너튜브 회원 전체

• 모수: 모집단을 분석하여 알아낸 결과, 수치로 모집단의 특성값
  • ex) 모평균(𝜇), 모분산(𝜎2), 모표준편차(𝜎) 등

• 표본: 모집단을 대표할 수 있는 일부를 추출하여 연구나 조사를 실시하고자 할 때 선택한 모집단의 일부
• 확률적 표본추출 방법: 모집단으로부터 표본을 추출할 때 동일한 확률 아래서 표본을 구성하는 방법
• 비확률적 표본추출 방법: 모집단으로부터 표본을 추출할 때 확률과 대상없이 연구자나 조사자가 자신의 생각대로 표본을 뽑거나 연구나 조사 대상이 표본을 구성하는 방법

2-10. 기술통계

기술통계란? 여러가지 현상에 대해 수리적으로 정리, 분석, 예측하는 작업이다.
아래는 실습코드를 요약한 코드다.

중심경향도

• 표본의 중심을 설명하는 것이 대표값 이라고도 하며 중심경향도라고 부르기도 한다.
• 중심경향도의 예시는 다음과 같다.
  • 평균, 중앙값, 최빈값

산포도

• 표본이 퍼진 정도를 구성하는 분포
• 산포도의 종류는 다음과 같다.
  • 분산, 표준편차, 범위 등

Library

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import platform
import numpy as np
import warnings
from matplotlib import font_manager, rc

# 한글 폰트 깨짐 방지
path = '/library/Fonts/Arial Unicode.ttf'

if platform.system() == 'Darwin':
    print('Hangul OK in your MAC!')
    rc('font', family='Arial Unicode MS')
elif platform.system() == 'Windows':
    font_name = font_manager.FontProperties(fname=path).get_name()
    rc('font', family=font_name)
else:
    print('Unknown system.. sorry')
plt.rcParams['axes.unicode_minus'] = False

# Data load
df = pd.read_csv('../data/gapminder.tsv', sep='\t')
df

Hangul OK in your MAC!

	country	continent	year	lifeExp	pop	gdpPercap
0	Afghanistan	Asia	1952	28.801	8425333	779.445314
1	Afghanistan	Asia	1957	30.332	9240934	820.853030
2	Afghanistan	Asia	1962	31.997	10267083	853.100710
3	Afghanistan	Asia	1967	34.020	11537966	836.197138
4	Afghanistan	Asia	1972	36.088	13079460	739.981106
...	...	...	...	...	...	...
1699	Zimbabwe	Africa	1987	62.351	9216418	706.157306
1700	Zimbabwe	Africa	1992	60.377	10704340	693.420786
1701	Zimbabwe	Africa	1997	46.809	11404948	792.449960
1702	Zimbabwe	Africa	2002	39.989	11926563	672.038623
1703	Zimbabwe	Africa	2007	43.487	12311143	469.709298

1704 rows × 6 columns

기초통계

# 기초통계 확인
df[['lifeExp']].describe()

	lifeExp
count	1704.000000
mean	59.474439
std	12.917107
min	23.599000
25%	48.198000
50%	60.712500
75%	70.845500
max	82.603000

# 대륙별 파이차트
df_group = df.groupby('continent').size()
labels = df_group.index
sizes = df_group.values
colors = sns.color_palette('pastel')[0:5]

plt.figure(figsize=(8, 6))
plt.pie(df_group, labels=labels, colors=colors, autopct='%.0f%%')
plt.show()

분포 확인

# 분포 확인
plt.figure(figsize=(8, 6))
sns.histplot(df['lifeExp'], alpha = 0.3, bins=7, color='Red')
plt.show()

이상치 확인

# 이상치 확인
plt.figure(figsize=(8, 6))
sns.boxplot(x='continent', y='lifeExp', data=df)
plt.show()

정규분포 생성

mu, sigma = 0, 0.1
s = np.random.normal(mu, sigma, 1000)

plt.figure(figsize=(8, 6))
sns.histplot(s, bins=30, kde=True, color="skyblue", stat="density")
plt.show()

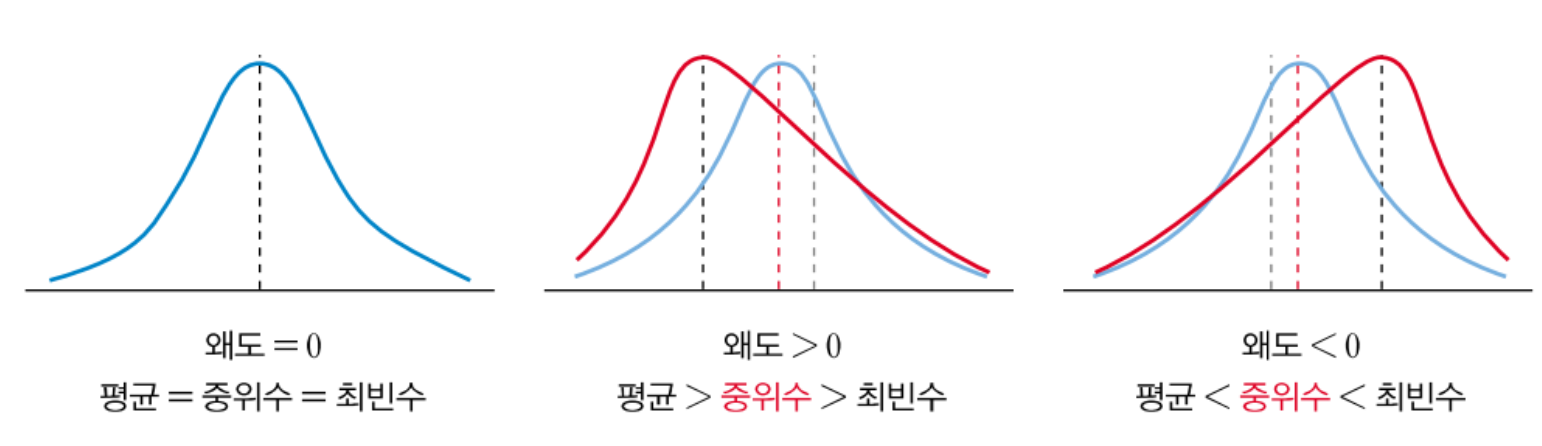
왜도 & 첨도

• 왜도: 자료의 분포가 어느 정도로 비대칭적으로 분포되어 있는지를 나타내는 통계 지표
• 첨도: 첨도는 분포곡선의 봉우리가 얼마나 뾰족한지를 나타내는 수치

warnings.filterwarnings('ignore')

# 데이터 생성
np.random.seed(42)
normal_data = np.random.normal(loc=0, scale=1, size=1000) # 정규분포
right_skewed = np.random.exponential(scale=1.0, size=1000) # 오른쪽 꼬리
left_skewed = -1 * np.random.exponential(scale=1.0, size=1000) # 왼쪽 꼬리

# 시각화
plt.figure(figsize=(18, 6))

# 1. 왼쪽 꼬리 분포
plt.subplot(1, 3, 1)
sns.histplot(left_skewed, bins=30, kde=True, color='skyblue', stat="density")
plt.title("왼쪽 꼬리 (Skew < 0)")

# 2. 정규분포
plt.subplot(1, 3, 2)
sns.histplot(normal_data, bins=30, kde=True, color='gray', stat="density")
plt.title("정규분포 (Skew = 0)")

# 3. 오른쪽 꼬리 분포
plt.subplot(1, 3, 3)
sns.histplot(right_skewed, bins=30, kde=True, color='salmon', stat="density")
plt.title("오른쪽 꼬리 (Skew > 0)")

plt.tight_layout()
plt.show()

2-11. Vector & Matrix

Scalar

• Scalar란 하나의 숫자로 표현되는 양을 의미
• ex) 사람의 체온을 측정하면 하나의 숫자로 표현

a = torch.tensor(36.5 )

Vector

• Vector란 순서가 지정된 여러 개의 숫자들이 일렬로 나열된 구조
• ex) 사람의 신체정보를 확인하기 위해 ‘키’, ‘체중‘, ‘허리둘레’, ‘시력(좌)’, ‘시력(우)’
  • 이라는 다섯 가지 항목을 측정하는 것

b = torch.tensor([175, 60, 81, 0.8, 0.9])

Matrix

• Matrix(행렬)란 동일한 크기를 가진 Vector들이 모여서 형성한, 행과 열로 구성된 사각형 구조
• ex) 그레이 스케일 이미지

c= torch.tensor([[77, 114, 140, 191], [39, 56,46, 119], [61, 29, 20, 33]])