[Deep Learning] Basic Model
[Deep Learning] CNN, RNN, LSTM, GRU 구조 이해하기
들어가며
이번 포스팅은 딥러닝 대표 모델인 CNN, RNN의 기본 구조와 동작 원리를 정리했습니다.
관련 용어는 딥러닝 기본 용어 정리를 참고
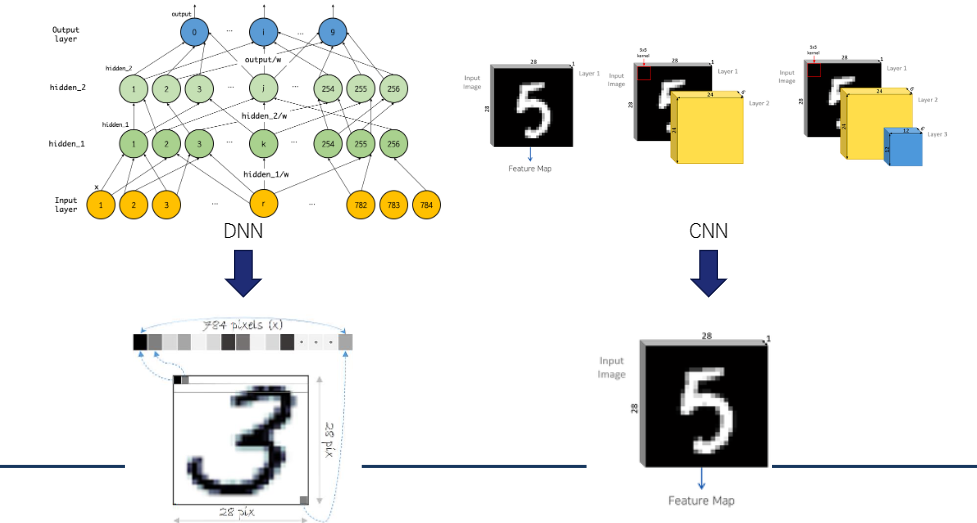
Convolutional Neural Network (CNN)
1. Convolution (합성곱) 연산
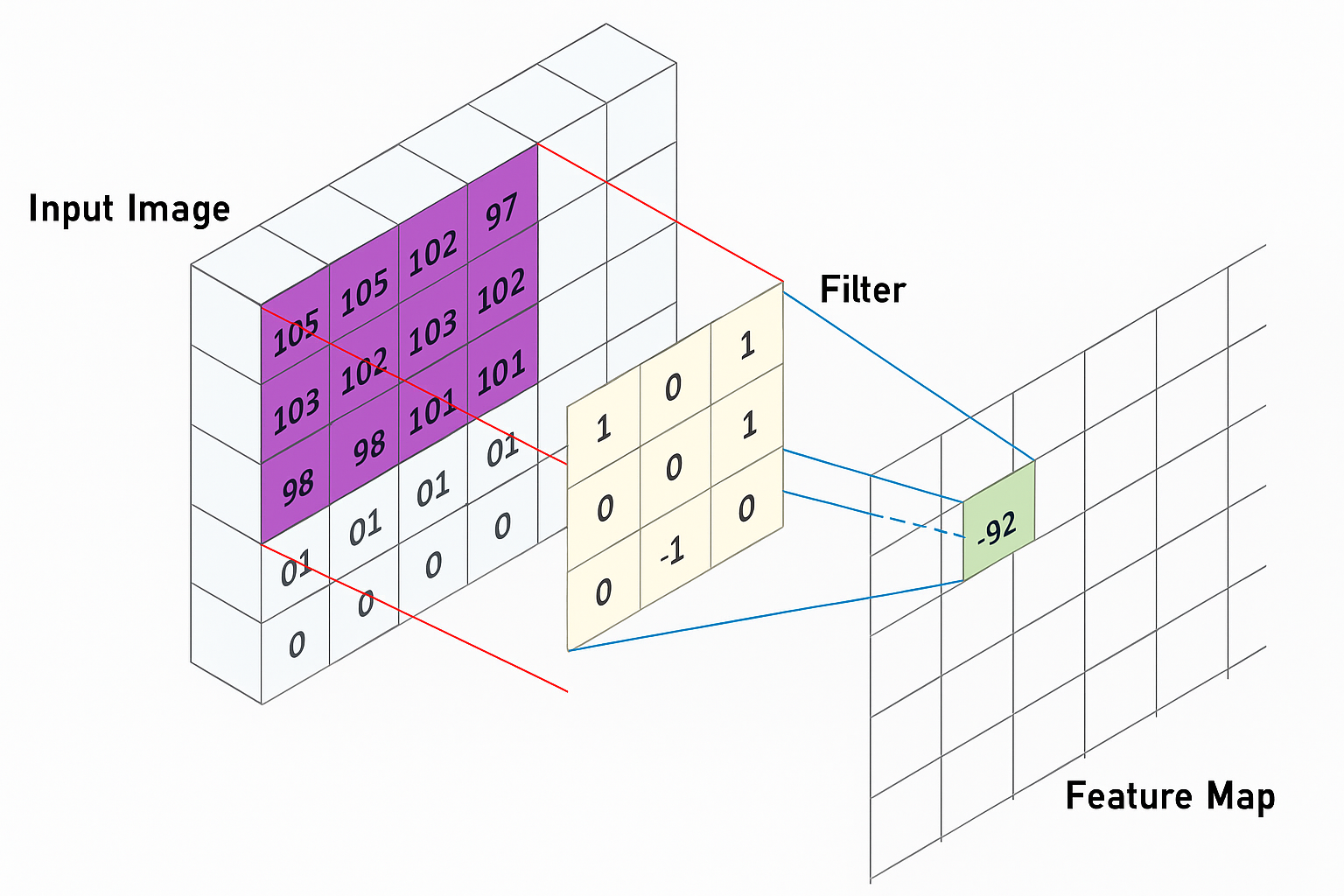
합성곱 연산은 입력 데이터에 Filter 혹은 Kernel를 적용하여 일정 크기의 Window를
왼쪽 위부터 오른쪽 아래로 이동시키며 적용한다. 이때 이동 간격은 보통 Stride라고 부른다.
- Input Image: 원본 이미지 데이터로, 2D 또는 3D 형태(RGB 등)를 가질 수 있다.
- Filter/Kernel: 특징을 추출하는 작은 행렬, 겹치는 영역끼리 곱하고 더해 특정 패턴에 반응하도록 학습된다.
- Feature Map: 필터 연산 결과로 나온 출력 행렬, 특정 특징이 강조되며, 필터 수만큼 생성된다.
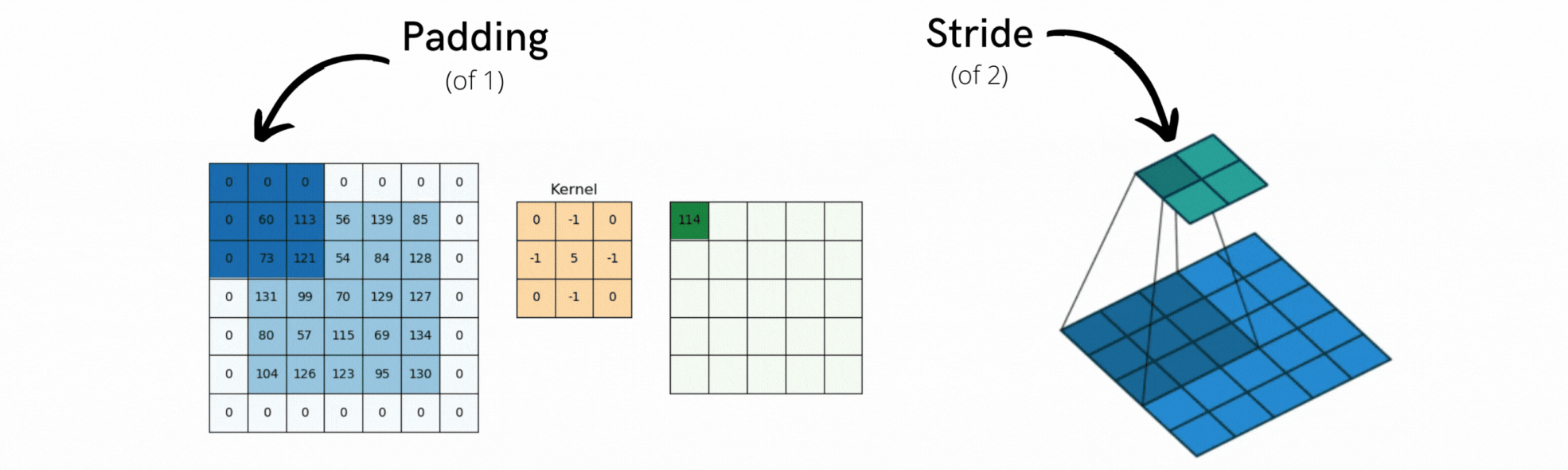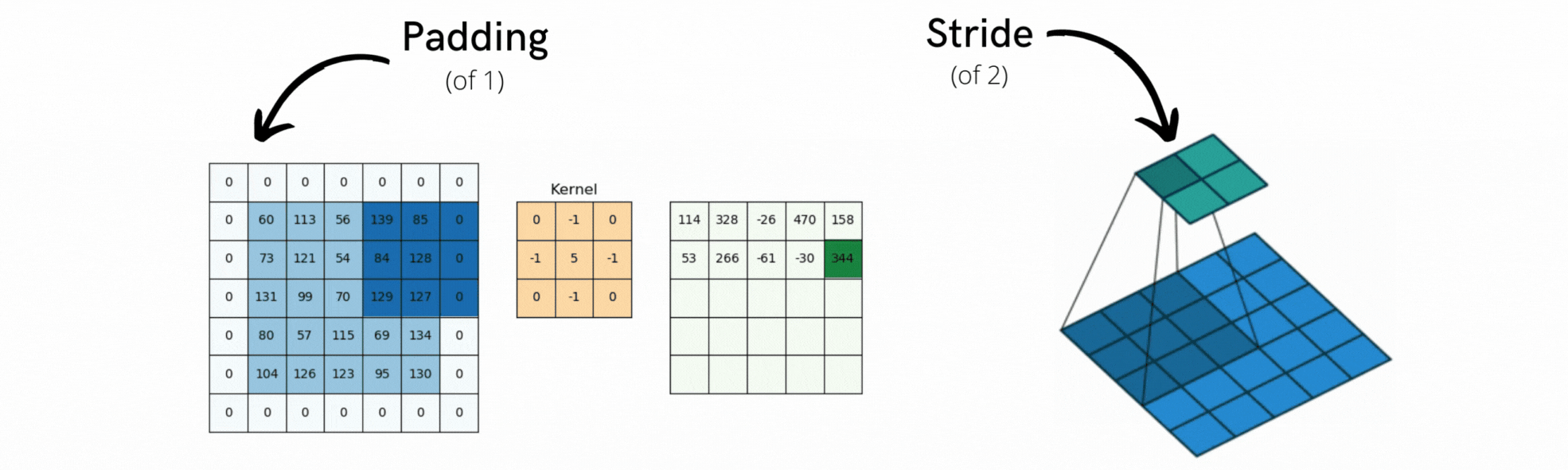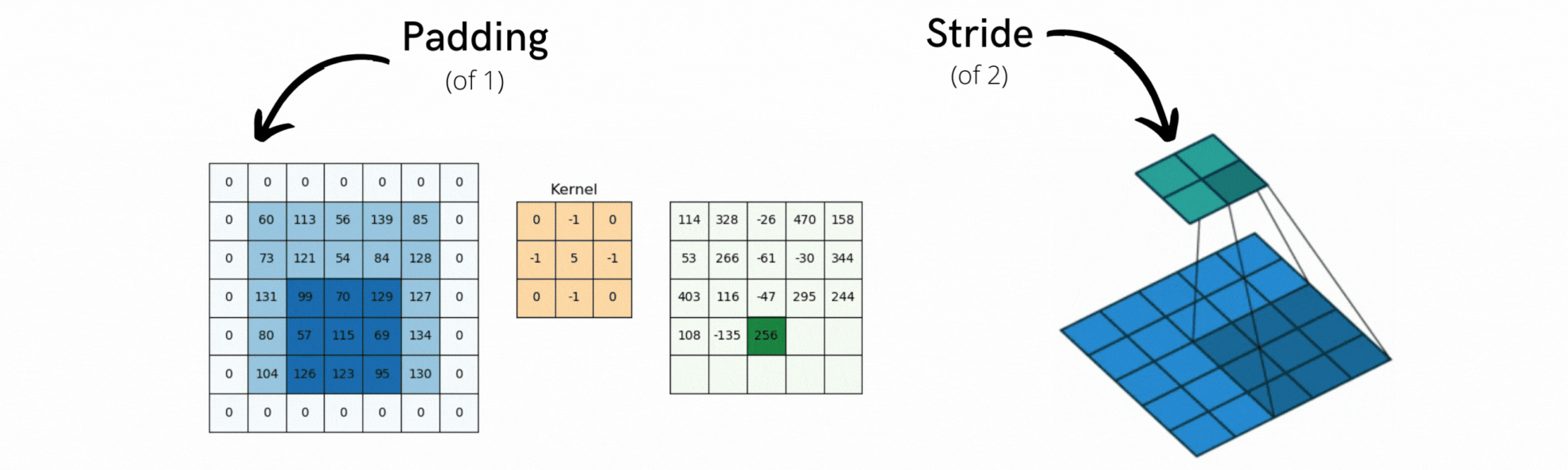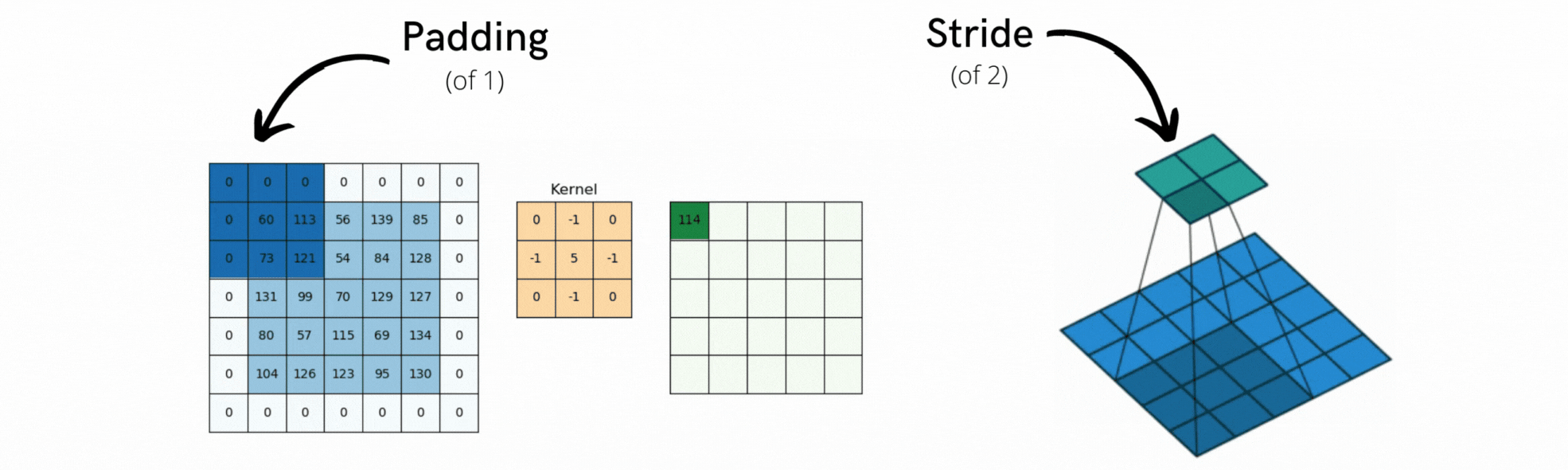
2. Padding
Padding은 합성곱 연산 전에 입력 데이터의 가장자리를 특정 값(보통 0) 으로 채우는 연산이다.
합성곱을 반복 적용하면 Feature Map 크기가 줄어들 수 있는데, 이를 방지하기 위해 사용된다.
- 너무 작은 Feature Map은 깊은 신경망 학습에 불리하다.
- 이 과정을 통해 필터가 가장자리 픽셀까지 충분히 연산에 포함되도록 도와주며,
- 출력 Feature Map의 크기 감소를 방지하거나, 특정 크기를 유지하는 데 사용된다.
same padding은 출력 크기를 입력과 같게 유지하고,valid padding은 패딩 없이 연산하여 크기를 줄인다.
3. Stride
Stride는 필터가 입력 이미지 위를 이동할 때 얼마만큼 건너뛰며 이동할지를 결정하는 값이다.
Stride가 커질수록 출력 크기는 줄어들고, 연산량도 줄어든다.
- 일반적으로
stride=1이면 필터가 한 칸씩 이동하며 모든 위치를 훑는다. stride=2이상을 사용하면 Feature Map 크기가 빠르게 작아진다.- Stride는 연산 효율을 높이는 데 사용되지만, 정보 손실의 가능성도 함께 커진다.
4. Feature Map 계산
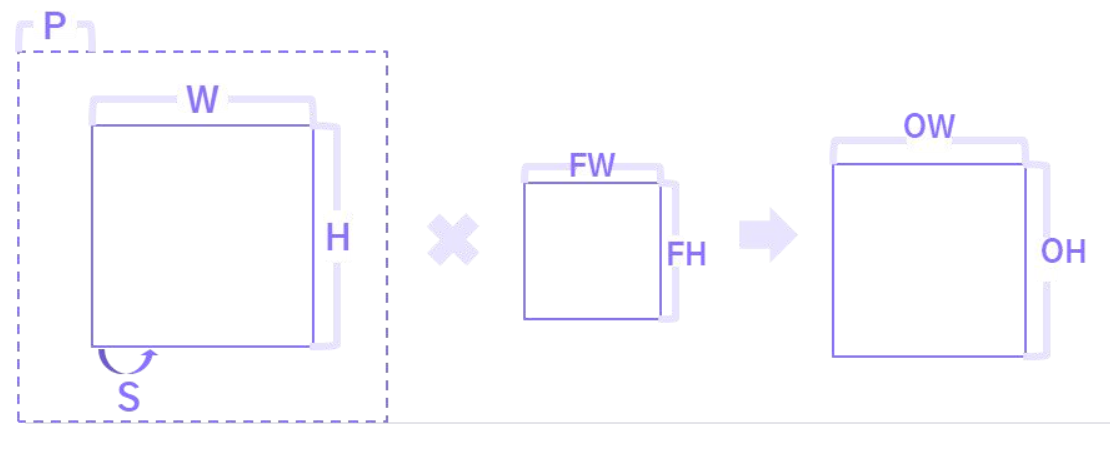
\[\text{Output Size} = \left\lfloor \frac{I + 2P - F}{S} \right\rfloor + 1\]Feature Map의 크기는 입력 이미지, Filter size, Padding, Stride 따라 결정된다.
일반적인 Feature Map 출력 크기 계산 공식은 다음과 같다.
- ( I ): Input size (Height 또는 Width)
- ( F ): Filter size
- ( P ): Padding
- ( S ): Stride
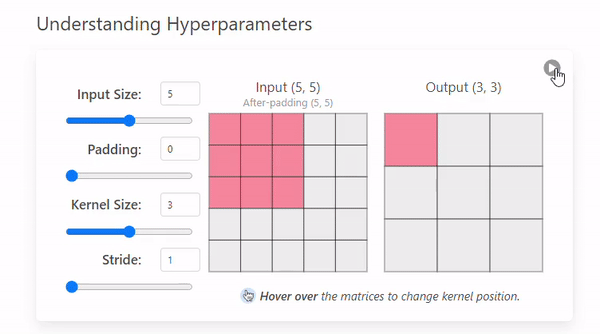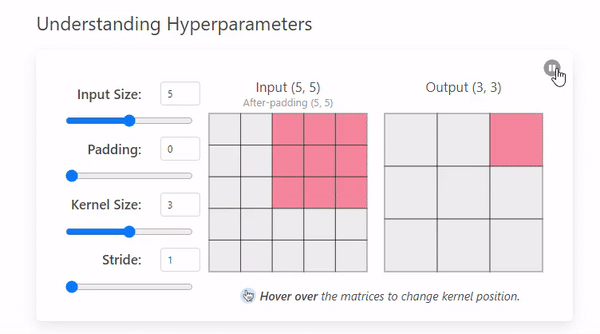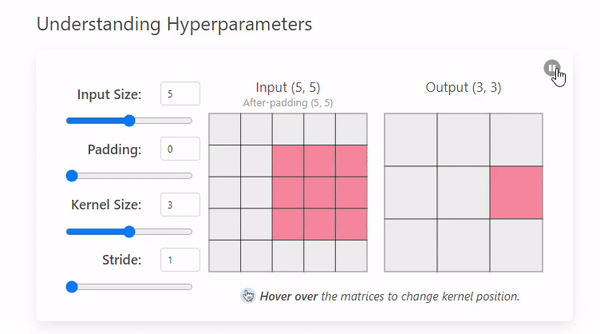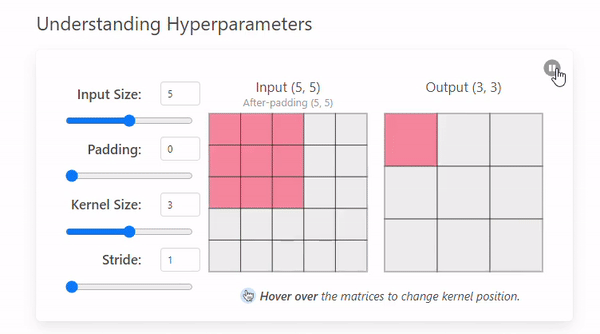
- 예를 들어, 5×5 입력 이미지에 3×3 필터, 패딩 1, 스트라이드 1을 사용하면 출력은 다음과 같다.
즉, 출력 Feature Map의 크기는 5×5로 입력과 동일하다.
따라서 패딩을 잘 조절하면 크기를 유지한 채로 연산할 수 있다.
5. Pooling (풀링)
Pooling은 가로, 세로 방향의 크기를 줄이는 연산으로 피처맵에서 중요한 정보를 추출하기 위해 사용
일반적으로 슬라이딩 윈도우 방식으로 동작하며, 주로 2x2, 3x3 크기의 윈도우를 사용한다.
Pooling은 연산량을 줄이고 과적합을 줄이는 데 효과적
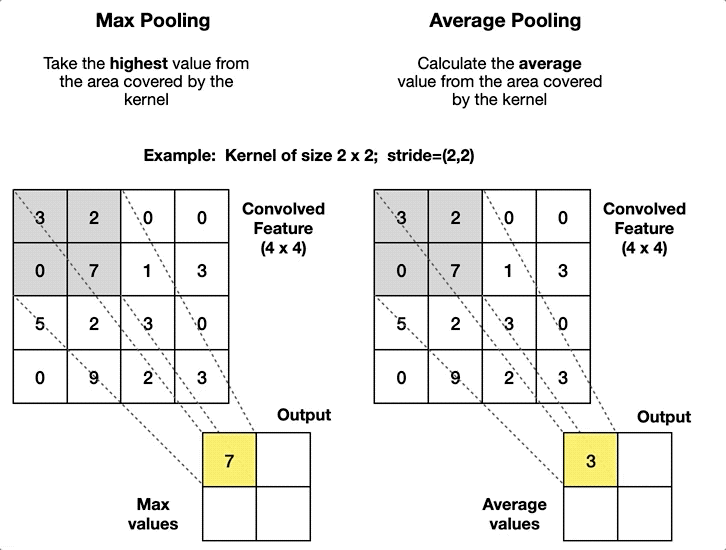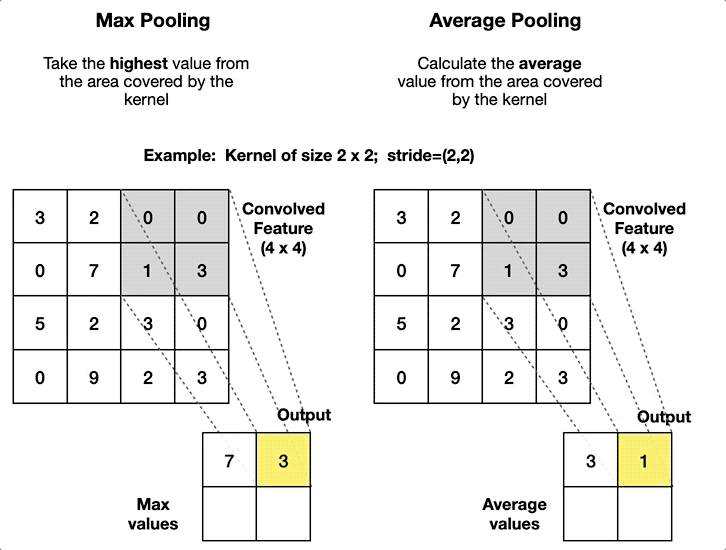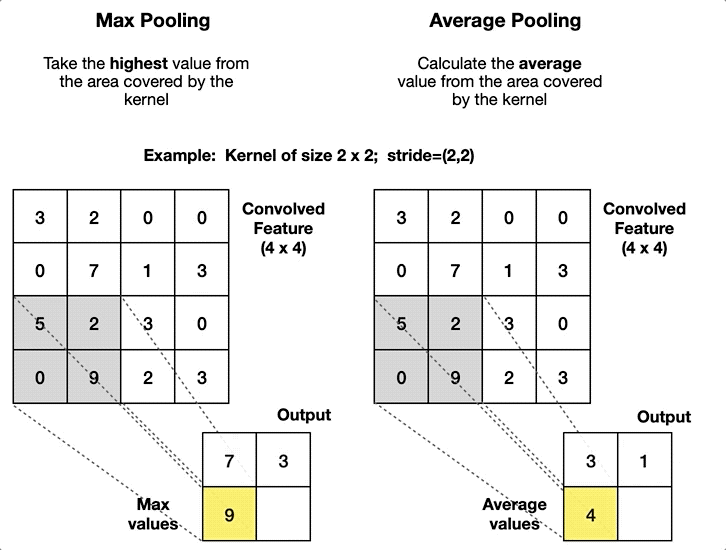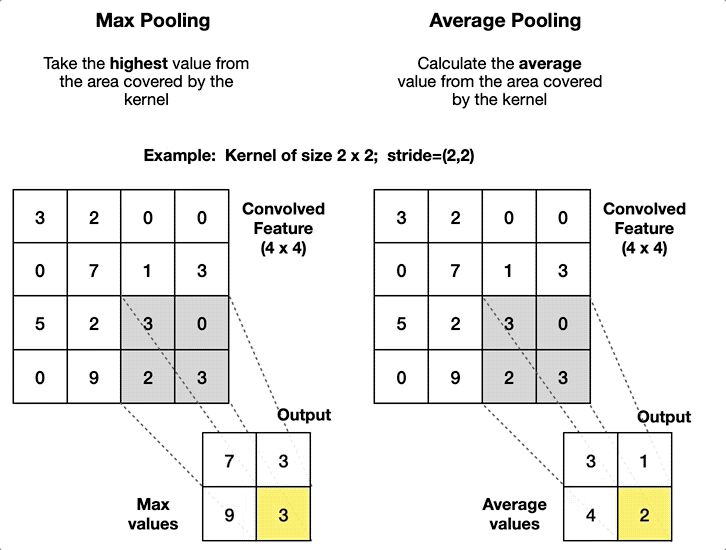
Max Pooling
- Feature Map에서 윈도우 영역 내의 최댓값을 취해 대표값으로 사용
- 일부 노이즈에 대해서는 덜 민감하게 반응할 수 있음
- 다만, 평균적인 정보나 배경 정보를 손실할 수 있다.
Average Pooling
- 윈도우 영역 내의 모든 값의 평균을 계산하여 대표값으로 사용
- 극단적인 값이 덜 민감
- 도드라진 특성이 덜 강조될 수 있다.
Recurrent Neural Network (RNN)
1. RNN 구조
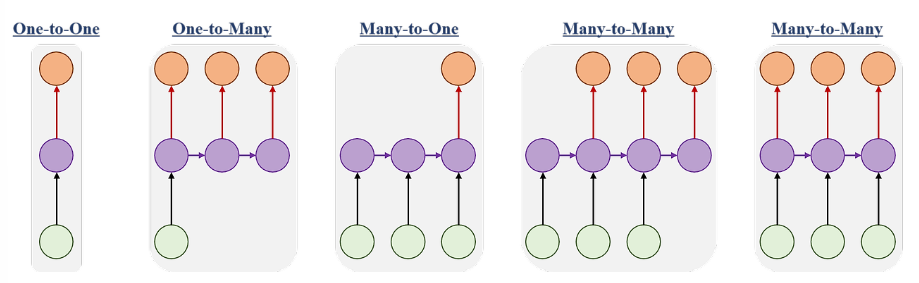
순환 신경망은 이전 시점의 정보를 현재 시점의 입력과 함께 처리하는 구조로 구성된다.
이를 통해 시퀀스 내의 문맥을 파악하고 정보를 기억하는 능력을 갖춘다.
- 은닉 상태(Hidden State)는 RNN의 핵심 요소로, 네트워크가 이전 시점의 정보를 얼마나 기억할지 결정한다.
- 이 상태는 시점마다 업데이트되며, 이전 시점의 은닉 상태와 현재 입력을 바탕으로 계산된다.
- 이 구조 덕분에 RNN은 시간 순서가 중요한 자연어 처리, 시계열 데이터 분석 등에 자주 사용된다.
- 일반적으로 tanh를 활성화 함수로 선택한다.
2. RNN 한계
시퀀스가 길어질수록 앞부분의 정보를 잊어버리는 문제가 발생한다.
이를 장기 의존성 문제라고 하며, 이 문제를 완화하기 위해 LSTM, GRU 같은 구조가 등장
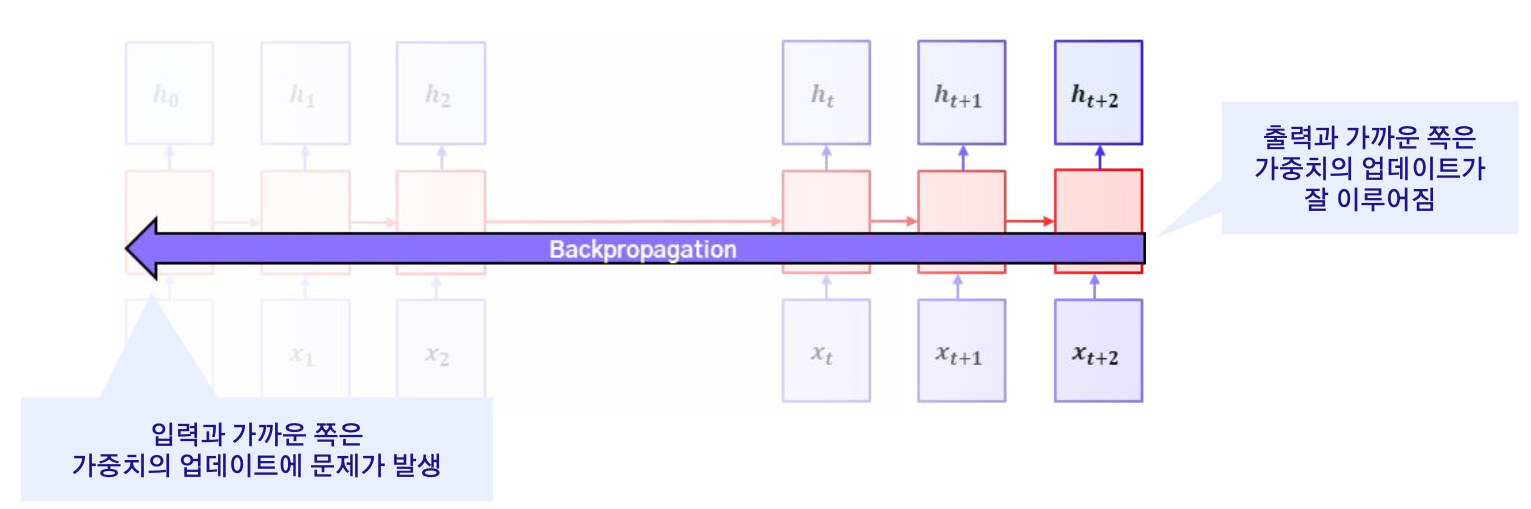
- 이 문제의 주요 원인은 역전파 과정에서 기울기가 매우 작아지는 현상(Gradient Vanishing) 때문이다.
- 시퀀스가 길어질수록 오차가 앞쪽까지 제대로 전달되지 않아 앞 시점의 정보가 학습에 거의 반영되지 않게 된다.
- 반대로, 경우에 따라 기울기가 급격히 커지는 문제도 발생할 수 있으며, 이는 학습 불안정으로 이어진다.
- 이러한 한계를 극복하기 위해 기억 셀을 도입한 구조인 LSTM과 GRU가 고안되었다.
3. LSTM (Long Short-Term Memory)
LSTM은 순환 신경망의 단점인 장기 의존성 문제를 해결하기 위해 설계된 RNN의 확장 구조이다.
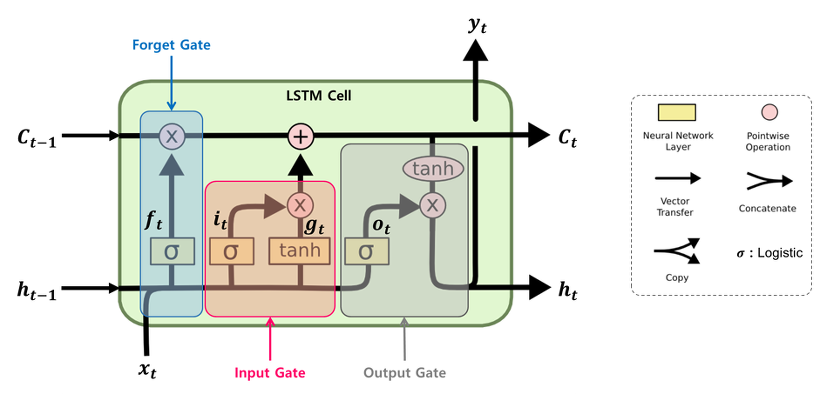
입력, 출력, 망각 등 3개의 Gate를 통해 정보 흐름을 조정하며
이로 인해서 시퀀스의 장기적인 정보를 잘 학습하고 유지할 수 있다.
- Forget Gate: 가장 첫 단계이며 이전 셀 상태 중 어떤 정보를 잊을지를 결정함
- Input Gate: 현재 입력과 이전 은닉 상태로부터 어떤 정보를 새로 저장할지 결정
- Output Gate: 다음 상태로 어떤 정보를 내보낼지 선택
이 구조를 통해 LSTM은 긴 시퀀스에서도 중요한 정보를 오래 기억할 수 있으며,
자연어 처리, 음성 인식, 시계열 예측 등에서 높은 성능을 보인다.
4. GRU (Gated Recurrent Unit)
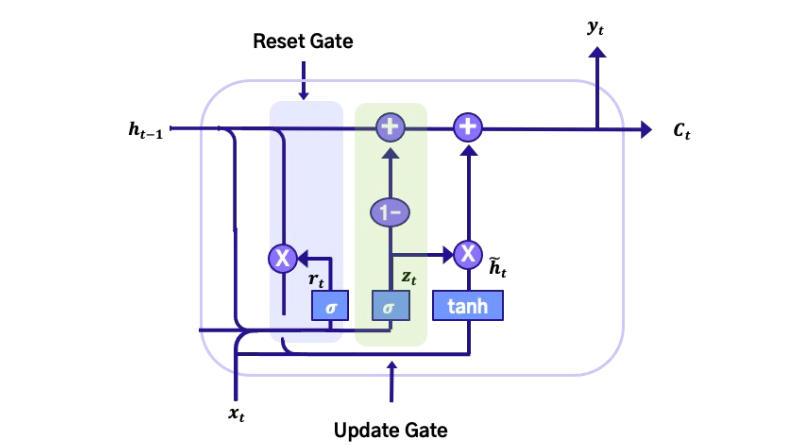
GRU는 LSTM을 보다 단순화한 구조로 Reset, Update Gate 두 가지 Gate만을 가지고 유사한 성능을 확보
이러한 구조 덕분에 LSTM 보다 적은 파라미터 수로 유사 성능을 낼 수 있어서 비용 효율적이다.
- Reset Gate: 이전 정보를 얼마나 ‘리셋’할지를 선택하는 Gate
- Update Gate: 새로운 정보를 얼마나 현재 상태에 반영할지를 결정
GRU는 LSTM보다 구조가 간단해 계산 속도가 빠르고, 학습 파라미터 수도 적다.
리소스가 제한된 환경이나 실시간 처리에 적합하며, 일부 문제에선 LSTM과 유사하거나 더 나은 성능을 보인다.
5. RNN, LSTM, GRU 구조 비교
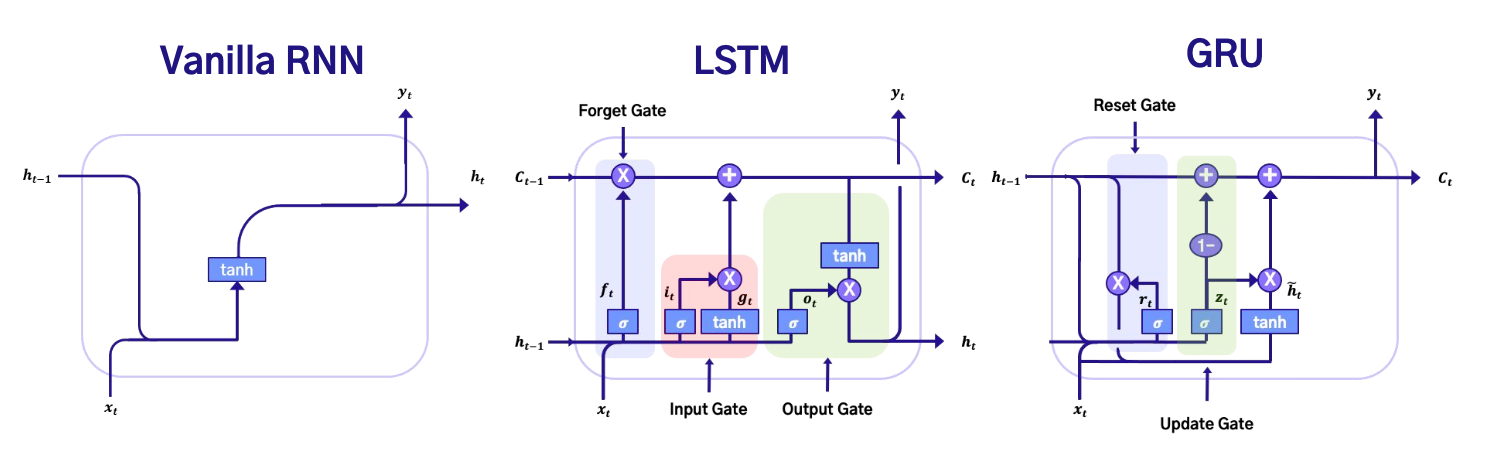
아래 그림은 Vanilla RNN, LSTM, GRU의 내부 구조를 한눈에 비교한 것이다.
각 구조가 어떻게 정보 흐름을 제어하고, 어떤 Gate를 사용하는지 시각적으로 확인할 수 있다.
- RNN: 단순히 이전 은닉 상태와 현재 입력을 결합하여 현재 은닉 상태를 계산
- 구조가 간단하지만, 장기 의존성 문제로 인해 정보 유지에 어려움이 있음.
- LSTM: Forget, Input, Output 세 가지 Gate를 사용하여 기억 셀(Cell state)을 관리
- 장기적인 정보 보존이 가능하고, Gradient Vanishing 문제를 완화함.
- GRU: LSTM보다 단순한 구조로 Reset, Update Gate만을 사용
- 연산량이 적고, 빠른 학습이 가능하면서도 비슷한 성능을 보이는 경우가 많음.