> >
Post

[빅분기] 필기 Chapter 09. 분석모형 평가 개선

[빅데이터분석기사] 필기 'Chapter 09. 분석모형 평가 및 개선' 내용을 정리했습니다.

Posted
Preview Image
By DoorNote
19 min read
[빅분기] 필기 Chapter 09. 분석모형 평가 개선

들어가며

빅데이터분석기사 필기 시험을 준비하며 공부한 내용을 Chapter 별 핵심 내용 기준으로 정리한 내용입니다.
교재는 이기적-빅데이터분석기사 필기-2024로 공부했습니다.



01. 분석 모형 평가

1. 평가 지표

분석모형의 답과 실제 답과의 관계 오차행렬을 통해 모델을 평가한다.

1-1) 지도학습-분류모델 평가 지표

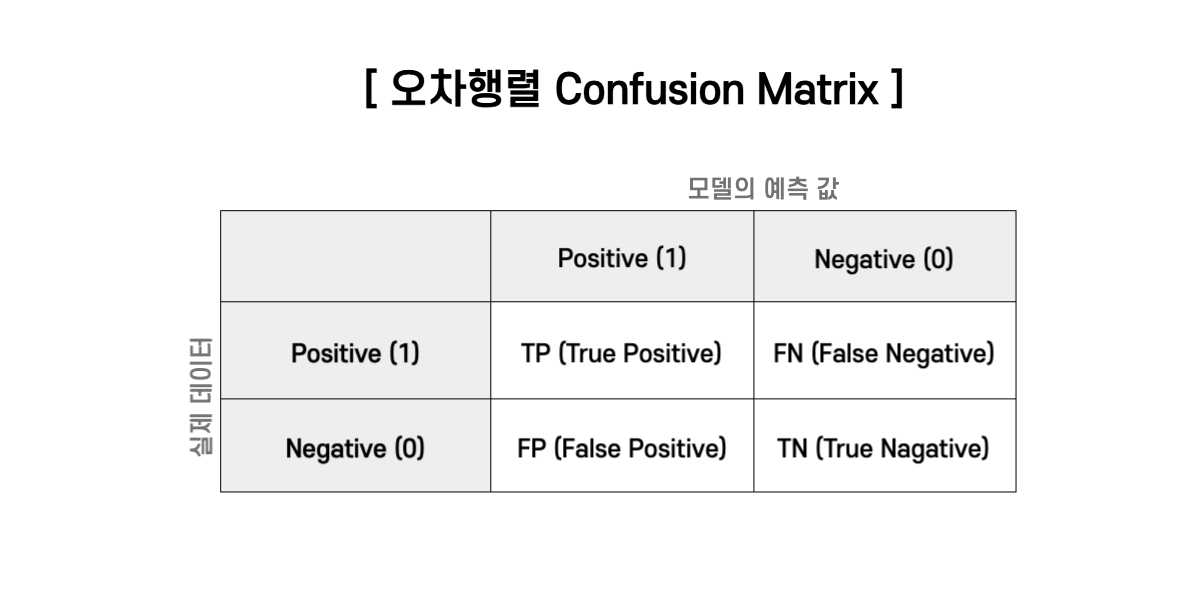
  • TP(True Positive): 실제 True인 답을 True라고 예측(정답)
  • FP(False Positive): 실제 False인 답을 True라고 예측(오답)
  • FN(False Negative): 실제 True인 답을 False라고 예측(오답)
  • TN(True Negative): 실제 False인 답을 False라고 예측(정답)


오차행렬(Confusion Matrix)

  • 훈련을 통한 예측 성능을 측정하기 위해 예측 값과 실제 값을 비교하기 위한 표


정확도(Accuracy)

  • 실제 데이터와 예측 데이터를 비교하여 같은 지 판단
  • 정확도는 모델의 전체적인 분류 성능을 나타낸다.
  • 높은 정확도는 모델이 입력 데이터를 정확하게 분류하는 능력을 의미
  • 클래스 불균형이 있는 데이터셋에서 잘못된 평가 결과를 얻을 수 있다.
  • 위 경우에는 정밀도, 재현율, F1 score 등 다른 지표들을 함께 고려
\[\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}}\]


정밀도(Precision)

  • Positive로 예측한 대상 중에 실제로 Positive인 값의 비율
  • 정밀도는 클래스 간의 불균형이 있는 데이터셋에서 유용하게 사용
  • ex: 암 진단 시나리오에서 암 환자를 정확하게 판단하는 것이 중요, 정밀도가 높은 모델을 선호
\[\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}\]


재현율(Recall)

  • 실제 Positive인 대상 중에 Positive로 정확하게 예측한 값의 비율
  • 높은 재현율는 모델이 실제 양성인 데이터를 놓치지 않고 잘 찾아낸다는 것을 의미
  • 재현율은 클래스 간의 불균형이 있는 데이터셋에서 유용하게 사용
\[\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}\]


F1 Score

  • 정밀도와 재현율을 결합한 조화평균 지표
  • 값이 클수록 모델이 정확하다고 판단할 수 있다.
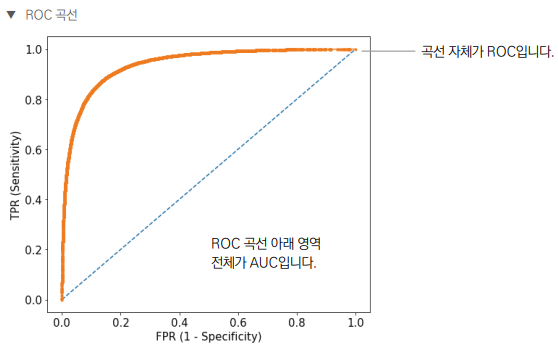
\[\text{F1 Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\]


ROC(Receiver Operating Characteristic)곡선

  • FPR(특이도)이 변할 떄 TPR(민감도)이 어떻게 변화하는지 나타내는 곡선
  • 임계값을 1~0 범주 이내 값으로 조정하면서 FPR에 따른 TPR을 계산하면서 곡선을 그림
  • ROC 곡선의 모양은 분류 모델 성능을 나타낸다.
  • 곡선은 왼쪽 상단 모서리에 가까울수록 좋은 성능을 가지는 모델임을 나타냄
  • 클래스 간의 불균형이 있는 데이터셋에서 유용하게 사용
\[TPR = \frac{TP}{TP + FN}\] \[FPR = \frac{FP}{FP + TN}\]



AUC(Area Under Curve)

  • AUC 값은 0에서 1 사이의 값을 가지며, 분류 모델의 성능을 종합적으로 평가하는 지표
  • AUC가 1에 가까울수록 분류 모델 성능이 우수하다고 할 수 있다.
  • 클래스 간의 불균형이 있는 데이터셋에서 유용하게 사용


1-2) 지도학습-회귀모델 평가 지표

회귀의 평가를 위한 지표는 실제값과 회귀 예측값의 차이를 기반으로 성능지표들을 수립, 활용

SSE(Sum Squared Error)

  • 실제값과 예측값의 차이를 제곱하여 더한 값
\[SSE = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2\]


MSE(Mean Squared Error)

  • 실제값과 예측값의 차이의 제곱에 대한 평균을 취한 값으로 평균제곱 오차라고도 한다.
\[MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2\]


RMSE(Root Mean Squared Error)

  • MSE에 루트를 취한 값으로 평균제곱근 오차라고도 함
\[RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}\]


MAE(Mean Absolute Error)

  • 실제값과 예측값의 차이의 절대값을 합한 평균값
\[MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|\]


결정계수 R²

  • 회귀모델이 실제값에 대해 얼마나 잘 적합하는지에 대한 비율
\[R^2 = 1 - \frac{SSE}{SST} = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}{\sum_{i=1}^{n}(y_i - \bar{y})^2}\]


평가지표 비교

지표내용
SSE오차제곱합
MSE평균제곱오차
RMSE평균제곱근오차
MAE평균절대오차
결정계수 R²모델의 설명력


1-3) 비지도학습-군집분석 평가 지표

  • 비지도학습은 지도학습과 달리 실측자료에 Label이 없으므로 모델에 대한 성능평가가 어렵다.
  • 군집분석에 한해 다음과 같은 성능 평가 지표를 참고


실루엣 계수

  • a(i)는 군집 내 데이터 응집도, b(i)는 군집 간 분리도
  • 0.5 보다 클 시 적절한 군집 모델, 0 이면 군집으로 분리가 의미 없음
\[s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}\]


Dunn Index

  • 군집 간 거리의 최소값을 분자, 군집 내 요소 간 거리의 최대값을 분포로 하는 지표
  • 군집 간 거리는 멀수록, 군집 내 분산은 작을수록 좋은 군집화
  • Dunn Index 값은 클수록 좋다.
\[D = \frac{\min_{1 \leq i < j \leq k} \delta(C_i, C_j)}{\max_{1 \leq l \leq k} \Delta(C_l)}\]



2. 분석모형 진단

2-1) 정규성 가정

분석을 진행하기 전에 데이터가 정규분포를 따르는지 검정하는 것으로 데이터 자체의 정규성을 확인

중심극한정리

  • 동일한 확률분포를 가진 독립확률변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다는 이론

정규성 검정 종류

  1. Shapiro-Wilk Test: 표본수가 2000개 미만인 데이터 셋에 적합
  2. 콜모고로프 스미르노프 검정: 표본수가 2000개 초과인 데이터 셋에 적합
  3. Q-Q 플롯: 데이터 셋이 정규분포를 따르는지 판단하는 시각적 분석 방법, 표본수가 소규모일 경우 적합


2-2) 잔차 진단

회귀분석에서 최적의 회귀선은 실측지와 예측치의 차이인 잔차를 가장 작게 해주는 선으로 잔차의 합은 0이며 잔차는 추세, 특정 패턴을 가지고 있지 않다.

  1. 잔차의 정규성 진단
    • 신뢰구간 추정과 가설검증을 정확하게 하기 위해 Q-Q Plot과 같은 시각화 됴표를 통해
    • 정규분포와 잔차의 분포를 비교
  2. 잔차의 등분산성 진단
    • 잔차의 분산이 특정 패턴이 없어 순서와 무관하게 일정한지 등분산성을 진단
  3. 잔차의 독립성 판단
    • 잔차의 독립성이란 자기상관의 여부를 판단하는 것
    • 시점 순서대로 그래프를 그리거나 더빈-왓슨-검정으로 패턴이 없다면 독립성을 충족한다고 할 수 있다.
    • 만약 독립성이 위배가 된다면 시계열 분석을 통해 회귀분석을 진행



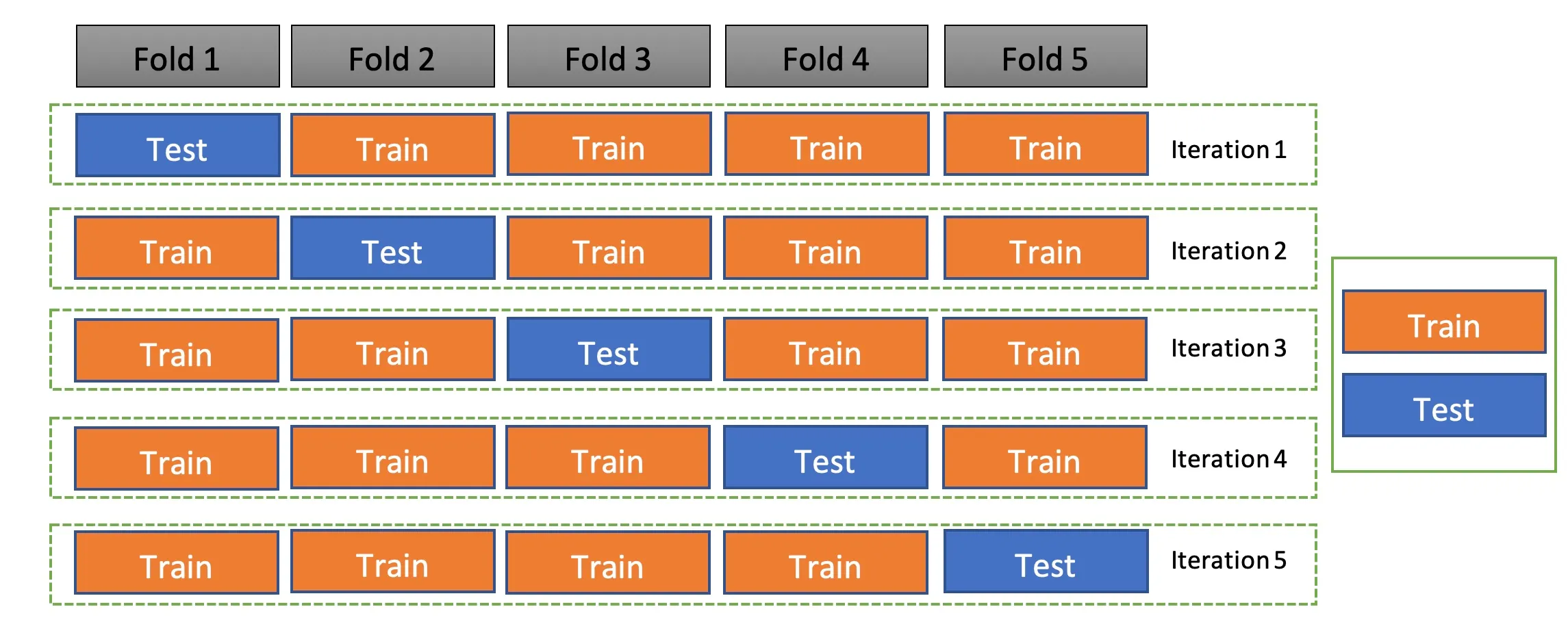
3. k-fold 교차검증(k-fold Cross Validation)

테스트 데이터셋에 과적합 되어버리는 결과가 생길 수 있을 떄 이를 방지하고자 나온 방법이 교차검증 기법이다.

k-fold

  • k개의 서브셋, k-1개의 훈련데이터, 1개의 검증데이터, 모든 데이터 셋을 평가에 활용하여 과적합 방지
  • 교차검증은 모든 데이터 셋을 평가에 활용하여 과적합을 방지할 수 있다.
  • 반복횟수 증가에 따른 모델 훈련과 평가/검증 시간이 오래 걸릴 수 있다.


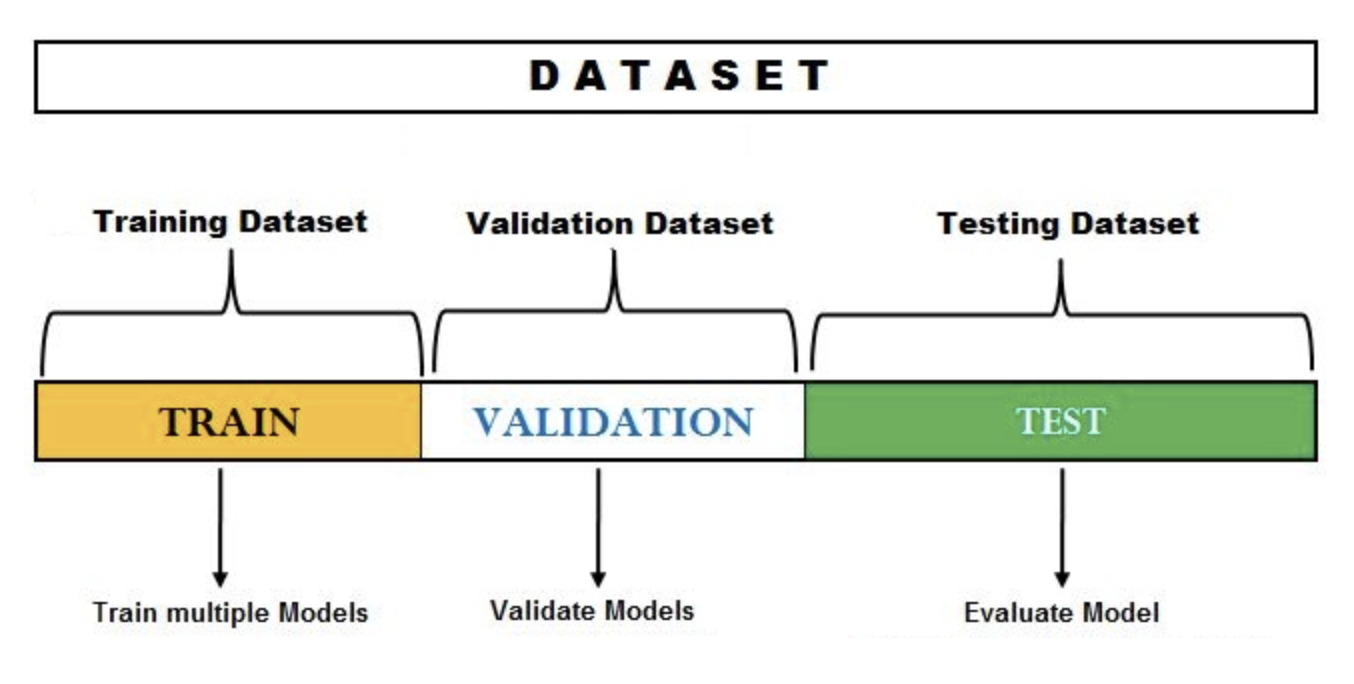
홀드아웃 기법

  • Train, Val, Test 데이터를 일정 비율로 지정
  • 크기가 작을수록 데이터를 나누는 방식에 따라 모델 성능 추정에 영향을 미칠 수 있는 단점이 있다.



4. 적합도 검정

데이터 분포가 특정 분포함수와 얼마나 맞는지를 검정하는 방법
일반적인 방법으로 정규성 검정이 있으며 정규분포를 가정하는 분석기법(t-Test, ANOVA, 회귀분석)이 적용될 시 데이터가 정규분포를 따라는가를 확인할 떄 사용된다.

카이제곱 검정

  • k 개의 범주별로 나뉘어진 관측치들과 동일한 범주의 가정된 분포 사이의 적합도 검정
\[\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}\]


콜모고로프-스미르노프 검정 (Kolmogorov-Smirnov Test)

  • 관측된 표본분포와 가정된 분포 사이의 적합도를 검사하는 누적분포함수의 차이를 이용한 검정법
  • 연속형 데이터에도 적용 가능

1표본 KS 검정

\[D = \sup_x | F_n(x) - F(x) |\]

2표본 KS 검정

\[D = \sup_x | F_1(x) - F_2(x) |\]




02. 분석모형 개선

1. 과대적합 방지

훈련 시에는 높은 성능을 보이지만, 테스트 데이터에 대해서는 낮은 성능을 보여주는 과적합을 방지하고, 일반화된 모델을 생성하기 위한 방향

1-1) 모델의 낮은 복잡도

드롭아웃(Dropout)

  • 신경망 모델에서 은닉층의 뉴런을 임의로 삭제하면서 학습하는 방법
  • 적은 수의 뉴런들로 학습을 진행할 때 시간이 오래 걸리는 단점이 있다.


1-2) 가중치 감소

  • 학습과정에서 큰 가중치에 대해서는 큰 패널티를 부과하여 가중치의 절대값을 가능한 작게 만듬
  • 규제란 과적합이 되지 않도록 모델을 강제로 제한하는 의미로 L1, L2 규제가 있다.


L1 규제

  • 손실함수에 가중치의 절대값인 L1 norm 을 추가 적용하여 대부분의 특성 가중치를 0 으로 만듬
\[\text{Loss}_{L1} = \text{Loss}_{\text{original}} + \lambda \sum_{j=1}^{n} |w_j|\]


L2 규제

  • 손실함수에 가중치에 대한 L2 norm 의 제곱을 더한 패널티를 부여
  • 가중치 값을 비용함수 모델에 비해 작게 만듬
\[\text{Loss}_{L2} = \text{Loss}_{\text{original}} + \lambda \sum_{j=1}^{n} w_j^2\]



2. 매개변수 최적화

신경망 학습의 목표는 손실 함수의 값을 최대한 낮추는 매개변수를 찾는 것
매개변수의 최적값을 찾는 과정을 매개변수 최적화라고 한다.

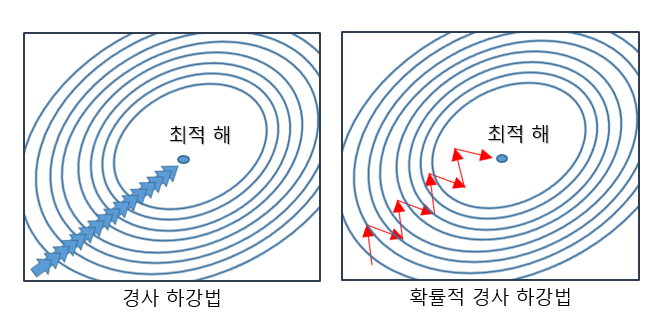
2-1) 확률적 경사 하강법(SGD)

  • 매개변수에 대한 손실함수의 기울기를 이용
  • 손실함수의 기울기를 따라 조금씩 아래로 내려가다가
  • 최종적으로 손실함수가 가장 작은 지점에 도달하도록 하는 알고리즘
  • 배치 경사 하강법과 비교하면, 단순하고 명확한 구조가 장점
  • 최소값인 0,0까지 지그재그로 이동, 매개변수가 방향에 따라 다른 기울기를 갖는 비등방성 함수인 경우 비효율적인 움직임을 보여줌


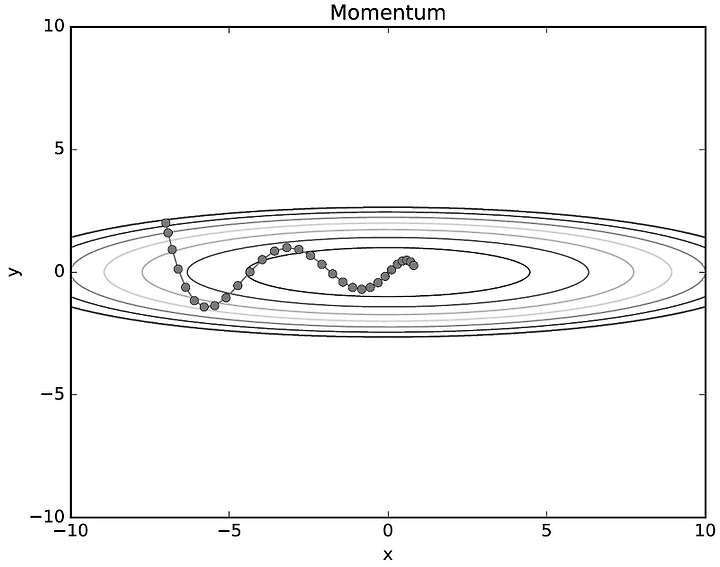
2-2) 모멘텀(Momentum)

  • 모멘텀은 운동량을 뜻함
  • SGD 에 속도 개념인 기울기 방향으로 힘을 받으면 가속되는 물리법칙을 알고리즘에 적용


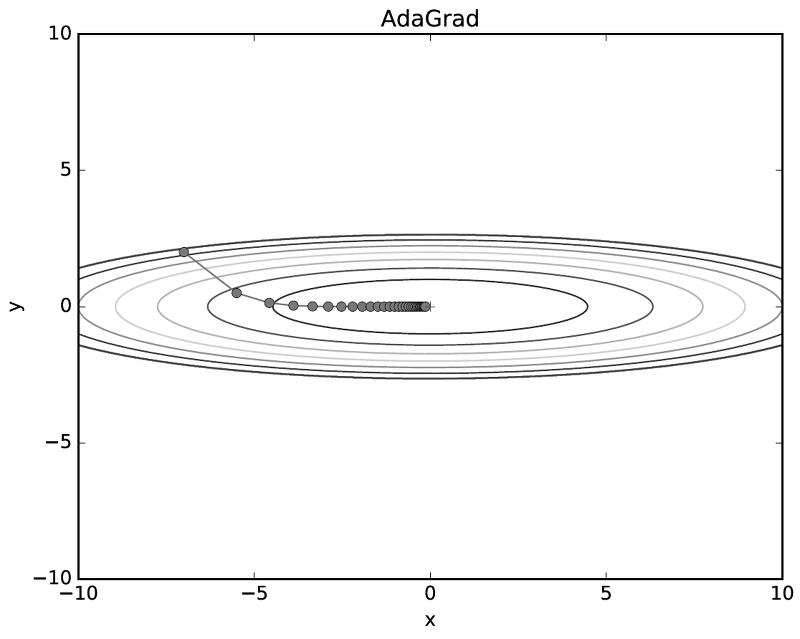
2-3) AdaGrad

  • 개별 매개변수에 적응적으로 학습률을 조정하면서 학습을 진행하는 알고리즘
  • 첫 부분에서는 크게 학습하다가 최적점에 가까울수록 학습률을 점차 줄여가며 작게 학습시킴


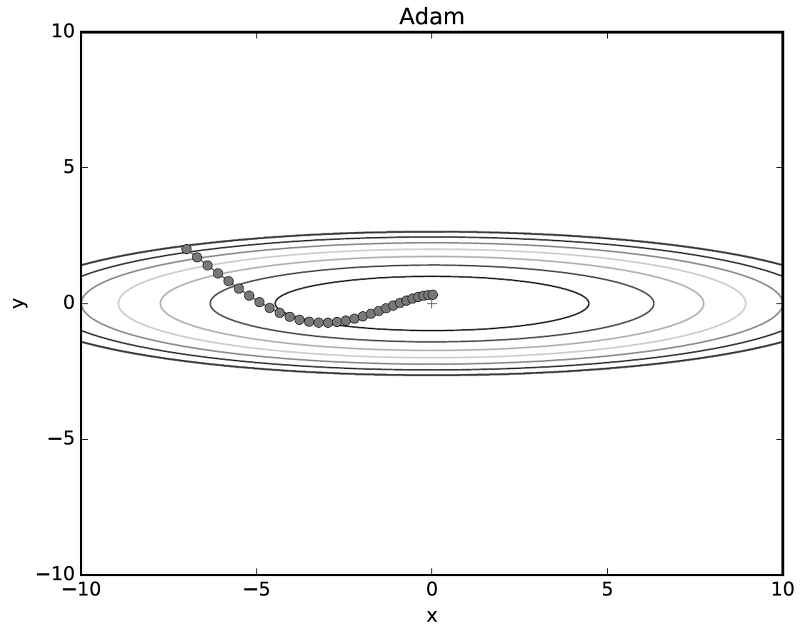
2-4) Adam

  • 모멘텀과 AdaGrad 를 결합한 방법론, 모멘텀과 비슷하게 진행되나 좌우 흔들림이 덜함
  • 학습률, 일차 모멘텀 계수, 이차 모멘텀 계수의 3가지 초매개변수 설정


2-5) 초매개변수 최적화

학습률

  • 기울기 방향으로 얼마나 빠르게 이동할지 결정, 작으면 학습 시간 길어짐
  • 학습률이 커지면 발산하여 학습이 제대로 이루어지지 않을 수 있다.


미니배치

  • 전체 학습 데이터를 주어진 배치 크기로 나눔
  • 큰 경우 병렬연산 구조를 사용할 때 효과적, 작은 경우 더 많은 가중치 업데이트 가능


Epoch

  • 학습의 조기 종료를 결정하는 변수


이터레이션

  • 하나의 미니배치를 학습할 때 1 iteration으로 1회 매개변수 업데이트 진행


은닉층 개수

  • 많아질수록 특정 훈련 데이터에 더 최적화
  • 모든 은닉층의 뉴런의 개수를 동일하게 하는 것이 가변적으로 하는 것보다 효과적



3. 분석모형 융합

앙상블 학습

  • 여러가지 분석 예측모형들을 만들고 해당 예측모형들을 결합하여 최종적인 하나의 예측모형을 만드는 방법
  • 치우침 있는 여러 모형의 평균을 취할 시 균형적인 결과를 얻음, 과적합 줄어듬


배깅

  • 복원 추출 방법으로 데이터를 샘플링, 모델링한 후 전체 결합하여 결과를 평균하는 기법


부스팅

  • 순서대로 모델들을 진행하는 방법
  • 이전 분류기의 학습 결과에 따라 다음 분류기의 학습 데이터의 샘플 가중치를 조정해 학습


랜덤포레스트

  • 결합분석 모형은 두 종류 이상의 결과변수를 동시에 분석할 수 있는 방법
  • 결과 변수 간의 유의성, 관련성을 설명할 수 있다.
자격증, 빅데이터분석기사
[빅분기]-필기 PART 04. 빅데이터 결과 해석
This post is licensed under CC BY 4.0 by the author.