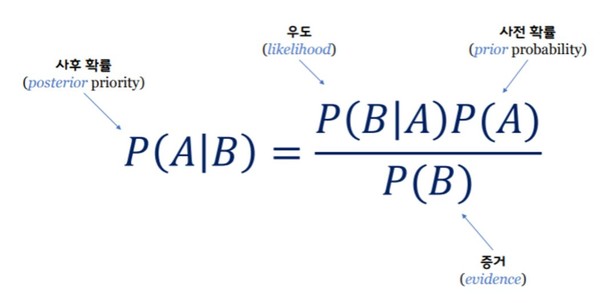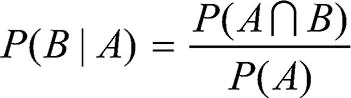[빅분기] 필기 Chapter 06. 통계기법의 이해
[빅데이터분석기사] 필기 'Chapter 06. 통계기법의 이해' 내용을 정리했습니다.
들어가며
빅데이터분석기사 필기 시험을 준비하며 공부한 내용을 Chapter 별 핵심 내용 기준으로 정리한 내용입니다.
교재는 이기적-빅데이터분석기사 필기-2024로 공부했습니다.
01. 기술통계
기술통계는 분석에 필요한 데이터를 요약하여 묘사, 설명하는 통계기법을 말한다.
분석 전 데이터의 특성을 찾아내서 그 특성의 정량화를 통한 체계적 요약이 필요
기술통계의 종류
| 종류 | 내용 |
|---|---|
| 중심화 경향 | 관찰 또는 수집된 데이터의 물리적 상대적 위치에 대한 정리 요약 |
| 분산도 경향 | 데이터들이 흩어진 정도에 대한 기술 및 요약 |
| 자료의 분포형태 | 자료의 분포가 대칭인지 치우쳐 있는지에 대한 기술 및 요약 |
1. 표본추출
- 모집단: 연구, 실험의 결과가 일반화된 큰 집단, 정보를 얻고자 하는 관심 대상의 전체집합으로 정의
- 표본: 여러 자료를 포함하는 모집단 속에서 그 일부를 끄집어 내어 조사한 결과로 원래 집단의 성질을 추측할 수 있는 자료로 정의
1-1) 전수조사와 표본조사
1. 전수조사
- 전수조사는 관심의 대상이 되는 모집단 전체를 대상으로 조사하는 것
- 인력과 예산이 비교적 많이 소요된다.
- 현실적으로 집단 내 모든 단위를 조사하는 것은 불가능한 경우가 많기에, 대부분의 통계조사는 표본조사에 의해 이루어진다.
- ex: 인구조사 등
2. 표본조사
- 표본조사는 관심의 대상이 되는 모집단에서 표본을 추출하여 표본을 대상으로 조사를 시행
- 기본적으로 전수조사가 정확한 결과를 도출할 수 있으나 비용문제 등의 제약사항이 존재
- 따라서 모집단의 일부가 전체를 대표할 수 있다는 근거가 명확하다면 일부의 표본으로 조사분석을 시행하고 모집단 전체의 분석결과로 사용이 가능
- 전수조사에 비해 비용 절감
- 조사결과의 신속성
- 조사규모가 크지 않기 떄문에 심도 있는 조사 가능
- 관리가 비교적 잘 되어 정확성 높음
1-2) 표본추출 오차
표본을 이용하여 모집단 특성을 추정함으로써 발생하는 모집단과 표본의 오차 범위 표본에서 선택된 대상이 모집단의 특성을 과잉 대표하거나 최소 대표할 떄 발생
1. 과잉 대표
- 중복선택 등의 원인으로 모집단이 반복, 중복된 데이터만으로 규정되는 현상을 지칭
2. 최소 대표
- 실제 모집단의 대표성을 나타낼 표본이 아닌 다른 데이터가 표본이 되는 현상
- 표본추출 시 표본의 크기보다는 대표성을 가지는 표본을 추출하는 것이 중요
1-3) 확률 표본추출 기법
모집단에 속하는 모든 추출단위에 대해 사전에 일정한 추출확률이 주어지는 표본 추출법
- 모든 표본들의 추출확률을 사전에 알 수 있다.
- 표본자료로부터 얻어지는 추정량의 통계적 정확도를 확률적으로 나타낼 수 있다.
1. 단순무작위 추출
- 통계조사에서 가장 기본이 되는 표본추출법이다.
- 모집단으로부터 무작위 추출하고 독립적 선택으로 편향성을 제거하여 난수를 이용하는 것이 기본이다.
- 추출 모집단에 대해 사전지식이 많지 않은 경우 시행하는 방법이다.
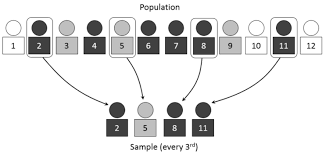
2. 계통추출
- 모집단에서 추출간격을 설정하여 간격 사이에서 무작위로 추출하는 방법이다.
- 만일 전체 모집단에 N개인 집단에서 K라는 추출간격으로 뽑는다면 N/K 수만큼 표본이 선택될 수 있다.
3. 층화추출
- 모집단을 서로 겹치지 않게 여러 층으로 나누어 분할된 층별로 배정된 표본을 단순 임의 추출법에 따라 추출하는 방법
- ex: 모집단의 남녀 성비가 3:2이면 표본의 성비도 3:2가 되도록 뽑는 경우
- 특징
- 단순임의추출법에 비해 추청 정도를 높일 수 있다.
- 추정뿐만 아니라 각 층별 추정결과도 얻을 수 있다.
- 표본의 대표성 제고 및 조사관리가 편리하고, 조사비용이 절감된다.
- 층화변수
- 모집단을 몇 개의 층으로 나누려고 할 때 각 추출단위가 어느 층에 속하는지를 구분하기 위해 기준으로 사용되는 변수
- 질적 층화변수: 변수값에 따라 층 구분
- 양적 층화변수: 층의 경계점을 나누는 방법 필요
4. 군집추출
- 모집단을 차이가 없는 여러 개 군집으로 나누어 군집의 단위의 일부 또는 전체에 대한 분석을 시행
- 모집단에 대한 구체적인 추출 방법론을 정하기 어려운 경우 사용하면 편리
- 표본크기가 같은 경우 단순 임의추출에 비해 표본 오차가 증대할 가능성이 있다.
1-4) 비확률 표본추출 기법
각 추출단위들이 표본에 추출될 확률을 객관적으로 나타낼 수 없는 표본추출법
- 일반적으로 모집단을 정확하게 규정지을 수 없는 경우, 표본오차가 큰 문제가 되지 않는 경우, 등에 사용
- 비용, 시간, 조사의 편리함 떄문에 자주 사용한다.
1. 간편추출법
- 응답자를 선정하는 데 있어서 조사원의 개인의 자의적인 판단에 따라 간편한 방법으로 표본을 추출하는 방법
- 얻어진 표본의 목표모집단을 얼마나 잘 대표하는지 알 수 없고, 얻어진 통계치에 대한 통계적 정확성을 평가할 수 없다.
- ex: 어떤 특정장소를 지나가는 사람들을 대상으로 여론조사를 하는 경우
2. 간편추출법
- 조사자가 나름의 지식과 경험에 의해 모집단을 가장 잘 대표한다고 여겨지는 표본을 주관적으로 선정하는 방법
- 표본의 크기가 작은 경우에 조사의 오차를 좌우하는 요인은 추정량의 분산이 될 수 있다.
2. 확률분포
확률과 확률분포는 모집단에 대한 추측 및 추론이 얼마나 정확한지에 대한 논리적 타당성을 제시하는 도구이다.
- 기술통계: 분석에 필요한 데이터를 요약하고 묘사, 설명하는 통계기법
- 추론통계: 표본에 내포되어 있는 정보를 이용하여 모집단에 대한 과학적인 추론을 하는 통계기법
2-1) 확률의 개념
- 통계적 현상: 불확정 현상을 반복하여 관찰하거나 혹은 집단 안에서 대량으로 관찰하여 그 고유의 법칙성을 찾아내는 것이 가능한 현상을 지칭
1. 확률
- 확률은 통계적 현상의 확실함의 정도를 나타내는 척도
- 랜덤 시행에서 어떠한 사건이 일어날 정도를 나타내는 사건에 할당된 수들을 말한다.
- ex: 주사위를 던질 때 6의 눈이 나올 확률은 1/6이다.
- ex :전체 카드 52장 중 한 장 뽑았을 때 하트카드가 나올 확률은 13/52 = 1/4이다.
- n(S) = 전체 경우의 수
- n(A) = 원하는 경우의 수
2. 통계적 확률
- 사건이 일어나는 확률을 상대도수에 의해 추정
- ex: 동전을 100번 던졌더니 앞면이 48번 나왔다면?
- n = 100, rₙ = 48
- n = 총 실험 횟수
- rₙ = 그 중 사건이 실제로 발생한 횟수
- P = 100/48 = 0.48
3. 표본공간
- 통계적 실험에서 모든 발생 가능한 실험결과들의 집합을 의미
- 표본공간 자체는 전사건, 아무것도 포함하지 않는 사건은 공사건이라 하고 하나의 결과를 포함하는 사건은 근원사건이라고 한다.
- 표본공간이 S인 확률 실험에서 사건은 S의 부분집합
4. ✅ 조건부 확률
- 사건 B가 일어났다는 조건하에서 다른 사건 A가 일어날 확률을 말함
- 즉, 이미 어떤 조건(B)이 발생했다고 가정하고, 그 안에서 A가 발생할 확률을 계산
- ex: 주사위를 던졌을 때 짝수가 나왔다는 걸 알고 있을 때 그 숫자가 2일 확률은?
- B = 짝수일 확률 → 가능한 값: {2, 4, 6}
- A ∩ B = 짝수이면서 2인 경우 → {2}
- $P(2 \mid 짝수) = \frac{1}{3}$
- 핵심 = 조건이 주어졌기 때문에 전체 표본공간이 줄어든다는 것
5. ✅ 결합 확률
- 사건 A와 B가 동시에 발생하는 확률로 이를 확률의 곱셈 법칙이라고 한다.
- 즉, A와 B가 동시에 일어날 확률은
한 사건이 일어난 조건하에서 다른 사건이 일어날 확률 × 조건이 된 사건의 확률
6. ✅ 베이지안 정리
- 사건 B가 발생했을 때, 사건 A가 일어났을 확률을 계산
- 즉, 결과(B)를 알고 있을 때, 원인(A)이었을 가능성을 추론
- 💡 조건부 확률을 “역방향”으로 뒤집어 계산하는 공식
- ex: 병원에서 검사 결과가 양성(B)이 나왔을 때, 실제로 병에 걸렸을 확률(A)을 계산하는 데 사용
- $P(A \mid B)$ → 우리가 알고 싶은 것 (사후 확률)
- $P(B \mid A)$ → 실제로 A일 때 B가 나올 확률 (검사 정확도)
- $P(A)$ → A일 확률 (사전 확률, 예: 질병 확률)
- $P(B)$ → B가 일어날 전체 확률 (전체 양성률)
2-2) 확률변수
확률변수는 사건의 시행의 결과를 하나의 수치로 대응시킬 때의 값을 의미하며, 일반적으로 대문자 X로 표기한다.
이산확률분포
- 확률변수가 취할 수 있는 값의 유한한 확률분포
연속확률분포
- 확률변수가 취할 수 있는 값의 수가 무한한 확률분포
- 자유도(df): 표본에서 자유롭게 선택 가능한 값의 수
- 표본분포: 표본 통계량의 분포
- 모평균 vs 표본평균:
- 모평균의 크기: ( \mu )
- 표본평균의 크기: ( \bar{X} )
- 표준오차: ( \frac{\sigma}{\sqrt{n}} )
- 정규분포의 성질: 평균, 표준편차로 분포의 모양과 위치가 결정
- 표본비율: ( \hat{p} = \frac{x}{n} ), x는 성공한 횟수
02. 추론통계
1. 점추정
모수에 대한 즉 모평균이나 모표준편차 등과 같은 추정치를 이에 대응하는 통계량으로 추정하는 것
1-1) 추정량의 선택기준
- 모수: 모집단의 특성을 수치화하여 나타내는 것(평균, 분산)
- 불편추정량: 모집단의 모수 추정에서 추정량의 기대값이 모수와 같을 때 추정량
불편성
- 표본 통계량의 기댓값이 모수의 실제값과 같을 때 이 추정량은 불편성을 가진다.
효율성
- 추정량 중에서 최소의 분산을 가진 추정량이 가장 효율적이다.
✅ 모수와 추정량 정리
| 모수 | 추정량 |
|---|---|
| 모평균 $\mu$ 에 대한 점추정 | 표본집단의 표본평균 $\bar{x}$ |
| 모분산 $\sigma^2$ 에 대한 점추정 | 표본집단의 표본분산 $s^2$ |
| 모비율 $p$ 에 대한 점추정 | 표본비율 $\hat{p}$ |
1-2) 구간추정
- 구간추정:
점추정에 오차 개념을 도입해,
모수가 포함될 확률변수구간(신뢰구간)을 추정하는 방법
✅ 주요 개념 요약
편향(Bias): 기대하는 추정량과 모수의 차이
→ 편향이 0이면 불편추정량최대우도추정량(MLE):
표본이 관측될 가능성(우도)을 가장 크게 만드는 추정량
→ 보통 ( \hat{\theta} )로 표현
✅ 모평균 신뢰구간 정리
| 구분 | 신뢰구간 공식 |
|---|---|
| 모집단의 분산을 아는 경우 | $ \bar{X} - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} \le \mu \le \bar{X} + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} $ |
| 모분산을 모름 (표본 작음) | $ \bar{X} - t_{\alpha/2, n-1} \cdot \frac{S}{\sqrt{n}} \le \mu \le \bar{X} + t_{\alpha/2, n-1} \cdot \frac{S}{\sqrt{n}} $ |
| 모분산을 모름 (표본 큼) | $ \bar{X} - z_{\alpha/2} \cdot \frac{S}{\sqrt{n}} \le \mu \le \bar{X} + z_{\alpha/2} \cdot \frac{S}{\sqrt{n}} $ |
2. 가설검정
모집단에 대해 어떤 가설을 설정하고 그 모집단으로부터 추출된 표본을 분석함으로써 그 가설이 맞는지 틀리는지 타당성 여부를 결정하는 통계적 기법
- 검정통계량
- 연구자에 의해 설정된 가설은 표본을 근거로 하여 채택여부를 결정지을 때 사용되는 표본통계량을 말한다.
- 가설검정
- 채택여부를 결정짓는 일련의 통계적 분석과정을 가설검정이라 하며 몇 단계의 절차를 거져 검정이 수행
1-2) 가설검정의 절차
- 귀무가설 H0 : 현재 통념적으로 믿어지고 있는 모수에 대한 주장 또는 원래의 기준이 되는 가설
- 대립가설 H1 : 연구자가 모수에 대해 새로운 통계적 입증을 이루어 내고자 하는 가설
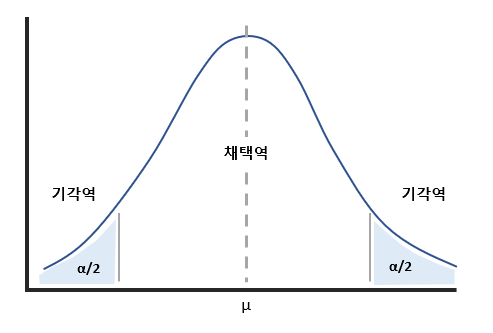
유의수준
- 유의수준: 귀무가설이 맞는데 틀렸다 결론 내리게 될 확률
- Success: 성공
- Type 1 Error: 제 1종 오류
- Type 2 Error: 제 2종 오류
| 검정결과 | 실제상황 $H_0$ | 실제상황 $H_1$ |
|---|---|---|
| $H_0$ 채택 | Success | Type 2 Error |
| $H_0$ 기각 | Type 1 Error | Success |
제 1종 오류
- 귀무가설이 참일 떄 귀무가설을 기각하도록 결정하는 오류
- 즉 대립가설을 채택
- 무죄인데 유죄라고 할 경우
제 2종 오류
- 귀무가설이 거짓인데 귀무가설을 채택할 오류
- 또는 대립가설이 참일 때 귀무가설을 채택하도록 결정하는 오류
- 즉 대립가설을 기각
- 유죄인데 무죄라고 할 오류
p-value
- 귀무가설을 기각하려고 할 때 필요한 최소의 유의수준
- p-value가 0.07인 경우, 귀무가설을 기각하면 잘못 기각할 확률이 0.07이다.
- p-value가 0.03인 경우, 귀무가설을 기각하면 잘못 기각할 확률이 0.03이다.
- 따라서 p-value가 작을수록, 즉 0에 가까울수록, 귀무가설을 기각할 수 있다.
📌 집단크기에 따른 검정통계량 설정
| 구분 | 통계량 수식 |
|---|---|
| 대표본 또는 모집단이 정규분포 | $Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \sim N(0,1)$ |
| 정규분포 따르면서 소표본 | $T = \frac{\bar{X} - \mu}{S / \sqrt{n}} \sim t(n-1)$ |
📌 표본에 따른 검정통계량 설정
1. 두 독립표본의 평균차이 검정
| 구분 | 통계량 수식 |
|---|---|
| 평균차 검정 | $T = \frac{\bar{X} - \bar{Y}}{S_p \sqrt{\frac{1}{n} + \frac{1}{m}}}$ |
| 풀링된 분산 계산 | $S_p^2 = \frac{(n-1)S_1^2 + (m-1)S_2^2}{n + m - 2}$ |
2. 대응표본의 평균차이 검정
| 구분 | 통계량 수식 |
|---|---|
| 평균차 검정 | $T = \frac{D}{S_D / \sqrt{n}}$ |
| 대응 표본 분산 계산 | $S_D^2 = \frac{\sum (D_i - \bar{D})^2}{n - 1}$ |
3. 분산에 대한 가설검정
| 구분 | 통계량 수식 |
|---|---|
| 단일표본 모분산에 대한 $\chi^2$ 검정 | $ \chi^2 = \frac{\sum (x_i - \bar{x})^2}{\sigma_0^2} = \frac{\phi S^2}{\sigma_0^2} $ |
| 두 모분산비에 대한 $F$ 검정 | $ F = \frac{S_1^2}{S_2^2} $ |